[科普中国]-伽利略定理

伽利略定理(Galilei theorem)是著名的圆面积等分定理，若OA为⊙O的半径，点M，N为OA的三等分点，以OA为直径作半圆，且过点M，N作OA之垂线交半圆于点P，Q，则以O为圆心，OP，OQ为半径之圆，必将最初的圆面积三等分，此定理由伽利略(G.Galilei)提出1。

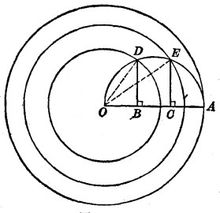
定理介绍定理1 以⊙O(R)的半径OA为直径作半圆，三等分OA于B、C，自B、C引OA的垂线交所作半圆于D、E(图1)，则以O为圆心，各过D和E点的两圆周必三等分原圆⊙O(R)的面积2。

定理2 甲乙两多边形彼此相似，假设甲形外切于某圆，乙形和某圆等周，则某圆的面积是甲乙两形面积的比例中项。

定理1和定理2均称伽利略定理，伽利略(Galilleo，1564-1642年)是十七世纪初叶意大利著名的物理学家和天文学家2。

定理的证明定理1的证明：

证明 连结OD和OE，则有

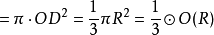所以 ⊙O(OD)的面积

的面积，

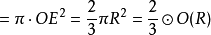⊙O(OE)的面积

的面积，

因此所作两圆⊙O(OD)和⊙O(OE)恰好三等分原圆⊙O(R)的面积2。

定理2的证明：

证明 设甲形外切于⊙O(R)，其半周为p，则其面积为:

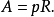乙形既和甲形相似(已知)，故也有内切圆⊙O'(R'。又乙形和⊙O(R)等周(已知)，可见乙形的半周为：

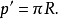从而乙形的面积为：

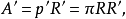于是

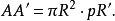
另一方面，由于甲乙两形相似，有

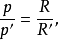那么

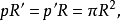所以

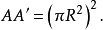
则定理得证2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所