[科普中国]-三角形外角定理

三角形外角定理(exterior angle theorem of a triangle)是平面几何的重要定理之一，指三角形的一个外角等于与它不相邻的两个内角的和。由此可得：三角形的外角大于任何一个与它不相邻的内角。

基本介绍三角形外角定理三角形的任意一个外角等于和它不相邻的两个内角之和。如图，△ABC的一个外角∠CBE=∠A+∠C。

这个定理的证明，如图所示，利用平行线的性质证明；也可以直接用三角形内角和定理证。

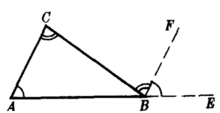
由三角形外角定理不难推出：三角形任意一个外角，大于和它不相邻的任意一个内角。如图，∠CBE>∠A，∠CBE>∠C1。

三角形外角定理的证明证法一利用三角形内角和定理证明有

∠1=∠A，∠2=∠B，∴ ∠1+∠2=∠A∠B(图2)2.

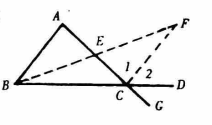
证法二全等形证法

如图2,设E为AC的中点，连BE且延长到F，使EF= BE，连CF。

在△ABE和△CEF中，

∵∠AEB=∠CEF，BE= EF，AE= EC

∴ △ABE≌△CEF

∴∠1=∠A

∴CF// AB

∴∠2=∠ABC，

∴∠1 +∠2=∠A+∠ABC，

即 ∠ACD=∠A+∠B.

推论及证明推论 三角形的一个外角大于任何一个和它不相邻的内角。

证法一根据三角形内角和定理推出三角形外角定理

有∠ACD=∠A+∠B，则

∠ACD>∠A(全量大于它的任一部分)

∠ACD>∠B2.

证法二全等形证

如上面图2，设E为AC的中点，连接BE且延长到F，使EF= BE，连CF，

在△AEB和△CEF中，

∠AEB=∠CEF，BE= EF，AE= EC，

∴△AEB≌△CEF，

∴∠ECF=∠A，

但∠ACD>∠ECF，

∴∠ACD>∠A.

其次，延长AC到G，得到∠ACD=∠BCG，作BC上的中线，并且把它延长，使延长的部分等于原来中线的长。同理可证∠BCG>∠ABC，由此可知∠ACD>∠ABC2。

证法三反证法

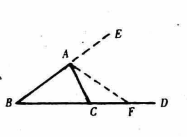
假设∠ACD ∠CAB，那么∠ACD=∠CAB，或∠ACD