[科普中国]-卢卡斯-卡纳德方法

在计算机视觉中，卢卡斯-金出方法是一种广泛使用的光流估计的差分方法，这个方法是由Bruce D. Lucas和Takeo Kanade发明的。它假设光流在像素点的邻域是一个常数，然后使用最小平方法对邻域中的所有像素点求解基本的光流方程。

介绍在计算机视觉中，卢卡斯-金出方法是一种广泛使用的光流估计的差分方法，这个方法是由Bruce D. Lucas和Takeo Kanade发明的。它假设光流在像素点的邻域是一个常数，然后使用最小平方法对邻域中的所有像素点求解基本的光流方程。1

通过结合几个邻近像素点的信息，卢卡斯-金出方法(简称为L-K方法)通常能够消除光流方程里的多义性。而且，与逐点计算的方法相比，L-K方法对图像噪声不敏感。不过，由于这是一种局部方法，所以在图像的均匀区域内部，L-K方法无法提供光流信息。

基本原理L-K方法假设两个相邻帧的图像内容位移很小，且位移在所研究点p的邻域内为大致为常数。1所以，可以假设光流方程在以p点为中心的窗口内对所有的像素都成立。也就是说，局部图像流（速度）向量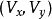须满足：

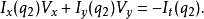
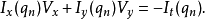其中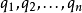， 是窗口中的像素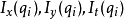，是图像在点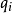和当前时间对位置x，y和时间t的偏导。

这些等式可以写成矩阵的形式Av=b，此处

此方程组的等式个数多于未知数个数，所以它通常是over-determined的。L-K方法使用最小平方法获得一个近似解，即计算一个2x2的方程组：

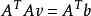或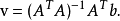

即计算：

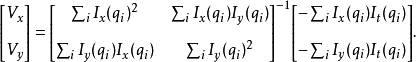
对i=1 到n求和。

矩阵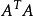通常被称作图像在点p的结构张量。

求光流的方法相位相关

块相关(误差绝对值和, 标准化互相关)

梯度约束-相关的对齐

卢卡斯-卡纳德方法（Lucas-Kanade Method）

霍恩·山克方法（Horn Schunck Method）

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所