[科普中国]-序贯结构

序贯结构是出现较早，最为常见和典型的卷积神经网络结构。序贯结构包含单输入与单输出，其神经网络由网络层堆叠而成。每一个网络层仅以上一层网络的输出为输入，并将经过处理后的输出送给下一层。序贯结构的典型代表模型是VGG系列网络。

定义序贯结构是一种卷积神经网络，由多个卷积层堆叠而成，下一层以上一层的输出作为输入。序贯结构只有单个输入和输出。早期的网络由于梯度弥散的问题，序贯结构无法堆叠很深。随着“ReLU”激活函数与更为科学的权重初始化策略的提出，序贯结构可以堆叠较深。但过深的网络仍然会出现训练困难甚至是网络退化的问题。网络退化指的是随着网络层数的加深，网络性能反而出现下降的现象。虽然如此，序贯结构因其形式简单，易于训练和调整，仍然作为一种经典结构被广泛使用1。

VGGNetSimonyan 等逐次在 AlexNet 中增加卷积层， 比较 6种不同深度的网络，研究网络深度的影响。结果表明神经网络越深，效果越好，当增加到 16、19 层时，效果提升明显，19 层的网络被称为 VGG-19。VGGNet严格采用 3×3 的卷积核， 步长 （stride） 和填补 （padding）都为 1；采用 2×2 的 max-pooling，步长为 2。相比于ZF Net 7×7 的卷积核，VGGNet 卷积核大小只有 3×3，使得模型参数更少， 而且连续两层的卷积层使其有 7×7卷积核的效果，之后人们通常也使用 3×3 的卷积核。VGGNet 模型用 Caffe 来实现，利用图片抖动来增加训练数据，在图片分类和物体定位任务都有很好的效果。

卷积神经网络卷积神经网络（Convolutional Neural Network, CNN）是一种前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元，对于大型图像处理有出色表现。

卷积神经网络由一个或多个卷积层和顶端的全连通层（对应经典的神经网络）组成，同时也包括关联权重和池化层（pooling layer）。这一结构使得卷积神经网络能够利用输入数据的二维结构。与其他深度学习结构相比，卷积神经网络在图像和语音识别方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比较其他深度、前馈神经网络，卷积神经网络需要考量的参数更少，使之成为一种颇具吸引力的深度学习结构。卷积神经网络包含卷积层、线性整流层、池化层和损失函数层。

卷积层

卷积层（Convolutional layer），卷积神经网络中每层卷积层由若干卷积单元组成，每个卷积单元的参数都是通过反向传播算法最佳化得到的。卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网路能从低级特征中迭代提取更复杂的特征。

线性整流层

线性整流层（Rectified Linear Units layer, ReLU layer）使用线性整流（Rectified Linear Units, ReLU） 作为这一层神经的激励函数（Activation function）。它可以增强判定函数和整个神经网络的非线性特性，而本身并不会改变卷积层。

事实上，其他的一些函数也可以用于增强网络的非线性特性，如双曲正切函数 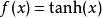，或者Sigmoid函数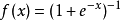。相比其它函数来说，ReLU函数更受欢迎，这是因为它可以将神经网络的训练速度提升数倍，而并不会对模型的泛化准确度造成显著影响。

池化层(Pooling Layer)

池化（Pooling）是卷积神经网络中另一个重要的概念，它实际上是一种形式的降采样。有多种不同形式的非线性池化函数，而其中“最大池化（Max pooling）”是最为常见的。它是将输入的图像划分为若干个矩形区域，对每个子区域输出最大值。直觉上，这种机制能够有效地原因在于，在发现一个特征之后，它的精确位置远不及它和其他特征的相对位置的关系重要。池化层会不断地减小数据的空间大小，因此参数的数量和计算量也会下降，这在一定程度上也控制了过拟合。通常来说，CNN的卷积层之间都会周期性地插入池化层。

池化层通常会分别作用于每个输入的特征并减小其大小。最常用形式的池化层是每隔2个元素从图像划分出 的区块，然后对每个区块中的4个数取最大值。这将会减少75%的数据量。除了最大池化之外，池化层也可以使用其他池化函数，例如“平均池化”甚至“L2-范数池化”等。过去，平均池化的使用曾经较为广泛，但是最近由于最大池化在实践中的表现更好，平均池化已经不太常用。

由于池化层过快地减少了数据的大小，文献中的趋势是使用较小的池化滤镜，甚至不再使用池化层。

损失函数层

损失函数层（loss layer）用于决定训练过程如何来“惩罚”网络的预测结果和真实结果之间的差异，它通常是网络的最后一层。各种不同的损失函数适用于不同类型的任务。例如，Softmax交叉熵损失函数常常被用于在K个类别中选出一个，而Sigmoid交叉熵损失函数常常用于多个独立的二分类问题。欧几里德损失函数常常用于结果取值范围为任意实数的问题。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所