[科普中国]-等角半正多角形

等角半正多角形(equiangular semiregular polygon)亦称等角半正多边形，是一种特殊的凸多边形，边数为偶数，相间的边相等，且所有的角都相等的凸多角形称为等角半正多角形。

基本概念凸多角形，若它的所有边都等，且所有角都等，则叫做正多角形。

同样，局部凸的星形多角形，若它的所有边都等且所有角都等，则叫做正星形多角形。

正多角形的概念可作如下的推广。

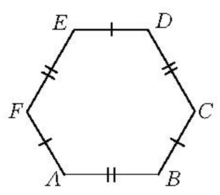
边数为偶数的凸多角形，假若其中相间的边相等且所有角都等，则叫做等角半正多角形。如图1，在六边形ABCDEF中，AB=CD=EF，BC=DE=FA，且∠A=∠B=∠C=∠D=∠E=∠F，因而它是等角半正多角形1。

边数为偶数的局部凸的星形多角形，若其中相间的边相等且所有角都等，则叫做等角半正星形多角形(例如图2的八角形)。

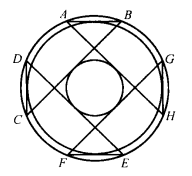
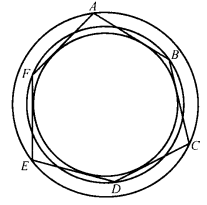
同样，凸的或星形的等边半正多角形，可以被定义如下：顶点数必须是偶数，所有边都等，相间的角相等；这时若是星形多角形还要假定它是局部凸的(例如，图3的六角形、图4的十角形)1。

相关结论定理1任意(凸的或星形的)正多角形或等角半正多角形可有一外接圆。

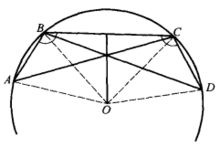
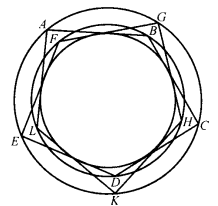
证明 假设A，B，C，D是所研究的多角形的四个相连续的顶点(图5)，O为三角形ABC的外接圆心。

三角形ABC与DCB相等(AB = DC，BC = CB，∠ABC=∠DCB)，因而三角形ABC的外接圆半径OA = OB = OC，与三角形DCB的外接圆半径相等。其次，二外接圆的圆心都在线段BC的垂直平分线上。最后，二圆心在直线BC的同侧，因为A和D二点在该直线的同侧(由于凸的或局部凸的多角形)。由此推得，圆周ABC与BCD的圆心重合。

可见通过三顶点A，B，C的圆周必通过点D，按照同样的考察方法可知该圆周也通过其余的顶点1。

定理2任意(凸的或星形的)正多角形或等边半正多角形可有一内切圆。

证明 假设AB，BC，CD和DE(图6)为一正多角形或等边半正多角形相连续的四边，K为直线AB和CD的交点，L为直线BC和DE的交点(如果相间而取的二边，如AB与CD平行，则边BC与DE亦将平行(因为这个多角形相间而取的角应相等)，点E与点A重合，我们便得一个菱形，对它来说，这定理也是正确的)。

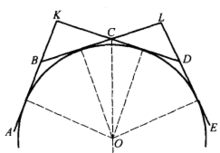
三角形BCK和DCL相等(BC = DC，∠KBC =∠LDC，∠KCB =∠LCD)，所以三角形BCK的边BC外的旁切圆半径等于三角形DCL的对应的旁切圆半径，因为该二圆心在∠BCD的平分线CX上，所以该二圆心重合，因而两圆周重合。

这样就得到了与射线BA，DE以及与边BC，CD相切的圆周，对于BC，CD，DE各边以及次一边EF重复同样的论述时，我们相信，该圆周与边DE及射线EF相切，等。

定理1及2系1 正多角形的外接圆心及内切圆心重合。

事实上，在这种情形下三角形OAB，OBC及OCD相等，因而外接圆心到各边的距离相等。

系****2 等角半正多角形，相间而取的边与同一圆周相切，这样就得到两个圆周，它们的圆心与外接圆心重合。

事实上，在图5上，三角形OAB与OCD相等，所以相间而取的边到外接圆心的距离相等。

系3 等边半正多角形，相间而取的顶点在同一圆周上，这样就得到两个圆周，它们的圆心与内切圆心重合。

事实上，在图6上有OA=OC=OE，OB=OD1。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所