[科普中国]-合同公理

合同公理(axiom of congruence)是建立图形相等关系的公理，它是希尔伯特公理体系中的第Ⅲ组公理。亦称“全合公理”、“叠合公理”、“全等公理”，是有关图形间“…与…合同”这种合同关系的公理。希尔伯特公理系统的合同公理是：(1)如果A、B是直线a上的两个点，A’是直线a'上的点，那么在直线a'上点A'任意指定的一侧，一定可以找到一个而且唯一的一个点B'，使得线段AB与线段A'B'合同；(2) 如果线段A'B'及A"B”都与同一条线段AB合同，那么A'B'与A"B"合同；(3)设AB和BC是直线a上的两个线段，没有公共的内部点，再设A'B'和B'C'是直线a'上的两条线段，也没有公共的内部点；如果AB、BC分别与A'B'、B'C'合同，那么AC也与A'C'合同；(4)如果在平面α上给了一个角∠(h,k)，在平面α'上给了直线a'，并且在平面α'上直线a'任意指定的一侧，设h'是直线a'上的一条射线，那么在平面α'上存在着唯一的一条射线k'，使得∠(h, k)合同于∠(h', k')；而且∠(h',k')的所有内部的点都在直线a'所指定的那一侧；(5)如果△ABC与△A'B'C'之间。AB、AC、∠BAC分别与A'B'、A'C'、∠B'A'C'合同，那么∠ABC、∠ACB分别与∠A'B'C'、∠A'C'B'合同。 合同公理解决了图形的运动问题1。

公理介绍合同公理是是希尔伯特公理体系中的第Ⅲ组公理，包括以下五条2：

1. 若A，B是直线a上的两点，A′是同一或另一直线a′上的一点，则在a′上点A′的已知一侧恒有一点B′，使线段AB合同于线段A′B′，记为AB≡A′B′。

2. 若两线段(可以相同)，都合同于第三线段，则这两线段也合同，即：若A′B′≡AB，A″B″≡AB，则有A′B′≡A″B″。

3.开线段(AB)，(BC)均在直线a上而无公共点，开线段(A′B′)，(B′C′)均在同一直线或另一直线a′上，亦无公共点，若AB≡A′B′，BC≡B′C′，则AC≡A′C′。

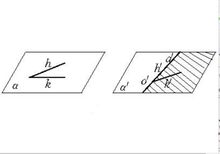
4.已知平面α上的一角∠(h，k)，在平面α′上有一直线a′，并在α′上指定直线a′的一侧，若在a′上有以O′为原点的一条射线h′，则在α′上恰有一射线k′，使∠(h，k)合同于∠(h′，k′)，且k′在a′的已知一侧，记为：∠(h，k)≡∠(h′，k′).对任何∠(h，k)，有∠(h，k)≡∠(h，k)且∠(h，k)≡∠(k，h)(如图1)。

5.对于两个三角形ABC和A′B′C′，若AB≡A′B′，AC≡A′C′，∠BAC≡∠B′A′C′，则∠ABC≡∠A′B′C′，∠ACB≡∠A′C′B′(如图2)。

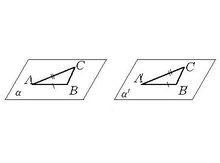
合同公理的推论定理1 若一个三角形中的两边合同，和这两边相对的两角就也合同；即：等腰三角形的底角相等3。

（关于所有公立以及定理的证明请参考相应书籍）3。

这个定理是公理5和公理4的末一部分的推论。

定理2(三角形的合同定理一)若两个三角形ABC和A'B'C'有下列合同式AB≡A'B'，AC≡A'C'，∠A≡∠A'，则三角形ABC就合同于三角形A'B'C'。

定理3 (三角形的合周定理二)若两个三角形ABC和A'B'C'有下列合同式AB≡A'B'，∠A≡∠A'，∠B≡∠B'，则三角形ABC就合同于三角形A'B'C'。

定理4 若∠ABC合同于∠A'B'C'，则∠ABC的邻补角∠CBD也合同于∠A'B'C'的邻补角∠C'B'D'。

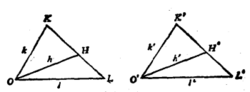
定理5 设h,k和l是一平面α上的、从一点O起始的三条射线(图3)，而且h', k”和l'是一平面α'上的、从一点O'起始的三条射线，又设h和k在l的同侧或异侧时，h'和k'也分别在l'的同侧或异侧。这时若∠(h,l)≡∠(h',l')和∠(k,l)≡∠(k’,l)，则∠(h,k)≡∠(h',k')3。

定理6 设平面α上的∠(h,k)合同于平面α'上的∠(h',k)，而且l是平面α上的、从角∠(h,k)的顶点起始的、在这角内的一条射线。 这时平面α'上恒恰有一条从∠(h',k')的顶点起始的在∠(h',k)内的射线l’，使∠(h,l)≡∠(h',l')和∠(k,l)≡∠(k',l')。

为了要得到合同定理三和角的合同的对称性，我们先从定理5导出下述定理:

定理7 若两点Z1和Z2在直线XY的异侧， 而且XZ1≡XZ2和YZ1≡YZ2，则∠XYZ1≡∠XYZ2。

定理8(三角形的合同定理三)若两个三角形ABC和A'B'C'的每对对应边合同，则这两个三角形就合同。

定理9若两个角∠(h'，k')和∠(h''，k'')，都合同于第三个角∠(h,k)，则∠(h'，k')也合同于∠(h''，k'')。

定理10 设给定了任意两个角∠(h,k)和∠(h',l')，设迁移∠(h,k)到沿着h’，而且在h'的l'侧时，所得到的射线是l，又迁移∠(h',l')到沿着h，而且在h的k侧时，所得到的射线是l，这时，若k’在∠(h',l')内，则l在∠(h,k)外。其逆也成立(图4)。

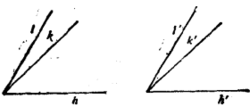
定理11所有的直角都互相合同。

定理12 (外角定理)在三角形中一个外角，大于其任一不相邻的内角。

下列诸定理是外角定理的重要推论。

定理13 在三角形中，长边所对的角大于短边所对的角。

定理14 若三角形有两角合同，则有两边合同。

这是定理1的逆定理，也是定理13的直接推论。

从定理12还能很简单地证得下述的、三角形的合同定理二的补充。

定理15 若两个三角形ABC和A'B'C'有下列合同式AB≡A'B'，∠A≡∠A'，∠C≡∠C'，则这两个三角形就合同。

定理16 每一线段都能二等分。

定理17 设有两个合同的点列，A, B, ..., K,L和A',B', ...,K', L',其中第一个中的点的顺序如下: B在A和C,或D,...,或K,或L之间，而且C在A,或B,和D,...,或K,或L之间，等等，则第二个点列中的点也有同样的顺序；那就是说,B'在A'和C'或D',...,或K', 或L'之间，而且C'在A',或B'和D', ..., 或K',或L'之间，等等。

定理18 设(A,B, C,..,L)和(A', B', C',...,L')是两个合同的平面图形。若P是第一个图形的平面上的一点，则第二个图形的平面上恒有一点P'存在，使(A, B, C,...,L,P)和(A',B',C' ,...,L',P') 还是合同的图形。若图形(A,B,C,..,L)至少含有不在同一条直线上的三点，则P'只有一个可能的作法。

定理19 设(A, B,C,...,L)和(A', B', C',...,L')是两个合同的图形。若P是任意一点,则恒有一点P'存在，使图形(A, B, C,...,L,P) 和(A, B,C, ...,L',P') 合同。若图形(A,B,C,...,L)至少含有不在同一平面上的四点，则P'只有一个可能的作法。

定理19说出了下述的重要事实：所有关于合同的空间事实，因此，空间中运动的性质，都是上述的直线的和平面的五条合同公理(结合着第一组和第二组公理)的推论。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所