[科普中国]-施瓦兹三角形问题

施瓦兹三角形问题(Schwarz triangle problem)是关于三角形的极值问题，在锐角三角形的内接三角形中，以垂足三角形的周长为最短，此问题最早由法尼亚诺(dei.T.G.C.Fagnano)提出，他用微积分的方法给出了一个解答，因此，这个问题也称为法尼亚诺问题。施瓦兹(H.A.Schwarz)在一篇论文中，利用垂足三角形的性质及反射原理巧妙地证明了这个问题，施瓦兹三角形因此而得名，他的证明后来被莫利(F.Morley)和莫莱(F.V.Morle)推广到2n+1角形的情况1。

基本介绍在已知的锐角三角形内，作顶点分别在其三边上的三角形，从中找出周长最短的一个，这是关于三角形的一个著名的极值问题，叫做施瓦兹(H.A.Schwarz)三角形问题。

可以证明，当内接三角形的顶点分别是已知锐角三角形的三条高的垂足时，所求得的三角形的周长最短。

该问题是意大利伯爵C.Fagnano(1682～1766)的儿子J.F.Fagnano(1715～1797)于1775年提出的，他给出了一个要用到微积分的证明。由于H.A.Schwarz(1843~1921)第一个用完全初等的方法给出了一个十分漂亮的解法，所以许多人把此问题称为Schwarz三角形问题，Schwarz的证明后来被美国人FrankMorley(1860~1931)推广到2n+1边形的情况。

在锐角△ABC中，若D、E、F分别是三条高AD、BE、CF的垂足，则在△ABC的所有内接三角形中，垂足三角形DEF的周长最短2。

施瓦兹三角形问题的证明证明一下面的证明源于H.A.Schwarz。

如图1，设△DEF是△ABC的垂足三角形，△PQR是任意内接三角形，将△ABC(连同△DEF、△PQR)作关于AC边的反射，再把所得图形(△AB'C)作关于B'C边的反射，再把所得图形(△A’B’C)作关于A'B'边的反射，再将所得图形(△A'B’C’)作关于A'C'边的反射，最后再把所得图形(△A'B''C')作关于B"C’边的反射，得△A"B"C'，经过这样五次反射后，我们得到如图1所示的连接在一起的六个全等的三角形(与△ABC全等)，以及分别与△DEF、OPQR相应的一系列内接三角形。

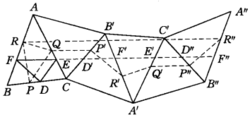
由于第一次反射使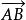 按逆时针方向旋转了角度2A，第二次反射使 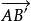按逆时针方向旋转了角度2B，第三次反射时 方向没有变化，第四次、第五次反射中 及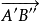 分别按顺时针方向旋转了2A和2B，故经过上述五次反射后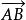， 的方向没有变化，所以A"B" // AB。

由于垂足三角形DEF有这样一个特殊性质：它的两边与△ABC的相应边成等角(即∠BDF=∠EDC，∠ DEC =∠FEA，∠EFA=∠DFB )，所以经第一次反射后，与DE相应的线段ED'在FE的延长线上，经第二次反射后，与DF相应的线段D'F"也在FE的延长线上，经第三次反射后，与EF相应的线段

F'E'也在FE的延长线上，以后两次反射也是如此，DE、DF的相应线段E'D"、D"F"都在FE的延长线上。因此，FED'F'E'D"F"是一直线段，且FF"等于△DEF的周长的两倍。

再来观察任意内接三角形PQR经上述五次反射后得到的图形，发现折线RQP'R'Q'P"R"的长度是△PQR的周长的两倍。显然该折线的长度不短于RR"，即△PQR的周长的两倍不短于RR"，由F"R" 平行且等于FR知RR"= FF"，可见△PQR的周长不短于△DEF的周长2。

证明二下面是Fagnano问题的另一种解法，这一解法属于法国的小Gabriel-Marie。

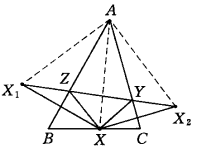
设△XYZ内接于△ABC，作出点X关于AB、AC的对称点X₁、X₂，则ZX₁= ZX，YX₂= YX，折线X₁ZYX₂的长度等于△XYZ的周长。显然，对于某个固定的点X，只有当Y、Z在线段X₁X₂上时，△XYZ的周长才能最小，其最小值为X₁X₂的长度，又由于AX₁= AX₂= AX，∠X₁AX₂=2A (定角)，

，X₁X₂的长度取决于AX的长度，只有当AX⊥BC时，X₁X₂才有最小值，因此，要使△XYZ的周长最短，必须AX⊥BC，同理，必须BY⊥AC，CZ⊥AB。故周长最短的内接三角形是△ABC的垂足三角形2。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所