单直尺作图(construction with a ruler)是一种作图方法,即只用一个直尺为工具的几何作图。早在1759年,朗伯(J.H.Lambert)在苏黎世为他出版的著作中,只用一个直尺解了一整套几何作图题,他是单直尺作图的鼻祖。此后,彭赛列(J.-V.Poncelet)也着手于用直尺作图的研究,于1822年在他的著作《图形的射影性质》中,论述了“在平面上已知一圆及其圆心时,则直尺和圆规能解的作图问题,只用直尺就能得解”。对这一事实,施泰纳(J.Steiner)在他的著作《一个定圆与直线可解的几何作图》中,给了进一步的论证1。
基本介绍用直尺、圆规解几何作图问题,是一种传统的规定,它是根据几何公理确定的。关于限制工具的作图问题,数学家们进行过许多研究,如尺规作图问题,尺规作图不能问题,单直尺或者单圆规作图问题,即只用一个直尺或只用一个圆规进行作图, 得出了一些重要的结果2。
人们往往认为由于允许使用工具种类越多,则能解的作图题范围越广,所允许使用的工具越少,则能解的作图题的范围便将缩小,其实并不如此。意大利数学家马奢罗尼(L.Mascheroni, 1750-1800)在1799年发表了他的著作《圆规几何学》,在这里他提出了所谓单圆规作图法。他证明了,如果我们认为“在平面上两点得到确定时,则过此两点的直线就被确定”,这时,所有用直尺和圆规能解的作图问题,用单圆规便都能作出。因为初等几何的作图,实际上是确定点的问题,用直尺和圆规所能确定的点,不外三种情形:
(1)直线与圆的交点;
(2)直线与直线的交点;
(3)圆与圆的交点。
这三种情形得到完成,用作图公法就都能得到完成。用单圆规可以完成(2),如果能用单圈规进行(1)、(2)两种惰形的作图,则上述“在平面上两点得到确定时,则过此两点的直线就被确定”中的结论就可得到证明。现在将(1)、(2)改述如下的形式:
(1)求作已知圆O (OA)与过二定点B、C的直线的交点。
(2)求作过二定点A、B的直线与过二定点C、D直线的交点。
马奢罗尼证明了这两个作图是可能的。因此,凡用直尺圆规能作的作图题,用单圆规都能作出。
法国的数学家彭赛列(Poncelet)在1822年,曾在他的著作《图形的射影性质》里,论述了“在平面上已知一圆及其圆心时,则直尺和圆规能解的作图问题,只用直尺就能得解”。当然,这里所说的圆的确定,只要知其圆心及圆周上的一点就可以了。这一事实,在1833年斯太纳(Steiner,德)的著作《一个定圆与直线可解的几何作图》里,有进一步的论述。因此,单直尺作图问题,是彭赛列和斯太纳共同完成的。为了证明单直尺作图的可能,只要能解下列的两个作图就可以了.
(1)求已知圆心为A及该圆周上一点B的圆与定直线g的交点。
(2)已知四点A、B、C、D时,求圆A(AB)与C(CD)的交点。
而这两个作图,被证明是可能的,因此单直尺的作图效能,也与直尺圆规相同2。
举例说明尺规作图历史悠久,影响深远,特别是古希腊三大几何难题更是吸引了无数数学爱好者,尺规作图看似简单,其实奥妙无穷,具有挑战性,能够培养数学思维和数学能力。随着人们数学水平的提高,从最开始的尺规作图,又引发出了单规作图、单尺作图等更高难度的作图。
下面介绍单尺作图的几个实例,并用面积法给出证明3。
【例1】已知线段AB和平行于AB的直线CD,仅用直尺求作线段AB的中点。
作法如图1:
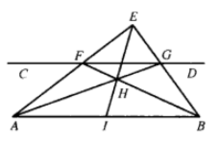
(1)作出线段AB和直线CD;
(2)在线段AB和直线CD外任取点E,联结AE、BE,分别交直线CD于点F、G;
(3)联结AG、BF,交于点H;
(4)延长EH交AB于点I,点I即为所求。
证明
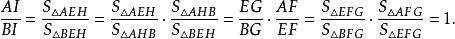
最后一步用到AB//CD,类似可证EH平分FG。这也是梯形中一个很有用的结论:延长梯形两腰所得的交点和梯形两对角线的交点的连线平分梯形的上底和下底。
1978年举行全国中学生数学竞赛时,数学大师华罗庚在北京主持命题小组的工作。著名数学家苏步青写信给华罗庚,建议出这个题目,但命题小组认为这个题目太难,改成“给出作好的图形,只要证明",可见此题难度不小。
【例2】已知线段AB和平行于AB的直线CD,仅用直尺求作线段AB的n等分点3。
作法 如图2:
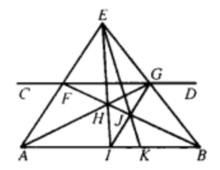
(1)按例1的方法作出AB的中点I;
(2)联结IG交BF于点J,延长EJ交AB于点K,则点K为AB的3等分点;
(3)类似操作即可得到线段AB的4等分点,5等分点...。
【例3】给定平行直线AB和CD,试过线外一点E,仅用直尺作平行于AB的直线。
作法 如图3,先按例1的方法作出AB的中点I;在AE的延长线上任取点J ,联结JI,交BE于点K;联结JB,与AK的延长线交于点L;直线EL即为所求3。
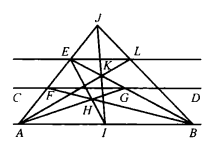
证明 因为
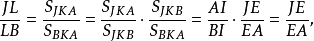 所以
所以
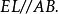
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国