[科普中国]-三角形奠基法

三角形奠基法(construction method by frist construct some triangle)是题解作图的一种常用方法。三角形是最简单的多边形，因此，只要很少的条件，就可把它作出来，在有些作图题中，先作成所求图形中的某个三角形，实际上便奠定了全部图形的基础，由此就可以逐步做出其余部分，这样的三角形，可称奠基三角形。利用奠基三角形作为基础来解作图题，叫做三角形奠基法。这个方法在作图中经常应用，有许多问题借助它可获得解决1。

基本介绍解某些作图题时，如果先作出图形中的某个三角形，然后在此基础上作出所要求作的图形，此种解作图题的方法称为三角形奠基法，该三角形称为作图的奠基三角形。

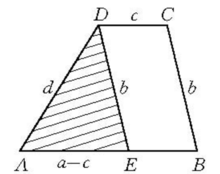
例如，已知四条线段a，b，c，d，求作梯形ABCD，使AB=a，BC=b，CD=c，DA=d，AB∥CD。该作图题的思路要点是：假设梯形ABCD已经作出，且AB=a，BC=b，CD=c，DA=d，作DE∥BC，则DE=b，AE=a-c，于是△AED可以确定(如图1)，并成为奠基三角形，在此基础上，所求作的梯形极易作出，当a，b，a-c中最大者小于其他两线段之和时该作图题有解，否则无解2。

例如，已知三角形的边a，以及这边上的高ha和中线ma，作此三角形。如下图所示。假定△ABC已作出。由条件知Rt△AHM是确定的，以该三角形为基础，作出BC=a，则得B、C两点。连结AB、AC，就得到△ABC3。

例题分析【例1】已知第一边的长，第二边上的高，第三边上的中线，求作三角形。

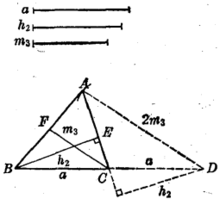
已知 三线段a、h、m3。

求作 △ABC，使边BC=a，高BE=h2，中线CF=m3。

分析 设图已成(图3)，在直角三角形△BCE中，已知斜边BC=a及一腰BE=h2，故此三角形得以确
定，确定此三角形后，若延长BC至D使CD=a，并连DA，则DA=2CF=2m3；因此A点可求。

作图 先作△BCE，使
∠BEC=90°，BE=h2，BC=a，
其次延长BC至D，使CD=a，最后以D为圆心、2m3为半径画弧设交直线CE于A，并连AB。这样作得△ABC就是所求三角形。

证明 作出△ABC的中线CF，由于BC=CD，得知

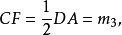又BE是△ABC的一高，且

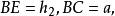故△ABC合乎所要求的条件。

推究 本题有无解答，只与a和h2的大小有关系；而解答个数，则和三已知线段的长短都有关联，其各种情形可归纳如下：

(1) a>h2时，若

1° h22m3，则无解。

(2) a=h2时，若

1° h2