ECT理论-牛顿引力理论(ECT Theory - Newton's Gravitation Theory)是描述在牛顿引力场中,粒子运动的拉格朗日量的计算与原理。
内容在牛顿引力场中,粒子运动的拉格朗日量为1:
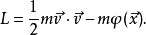 其中
其中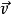 为粒子速度,
为粒子速度, 为牛顿引力势,粒子运动方程由最小作用量原理
为牛顿引力势,粒子运动方程由最小作用量原理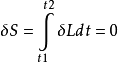 决定:
决定:
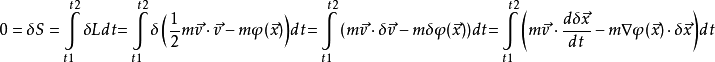
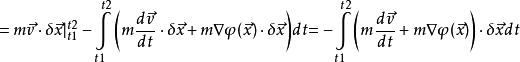 因此有:
因此有: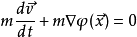 即:
即: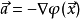 ,这是牛顿引力场中的粒子运动方程。
,这是牛顿引力场中的粒子运动方程。
考虑在牛顿引力场中无压理想流体的运动,则拉格朗日量变为:
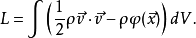 其中:
其中: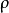 为流体质量密度,
为流体质量密度,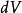 为体积元。 牛顿引力场本身的拉格朗日量为:
为体积元。 牛顿引力场本身的拉格朗日量为:
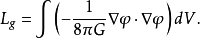
同时考虑引力场和无压理想流体,其总拉格朗日量为:
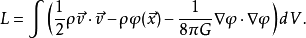
为了得到引力场的运动方程,只对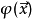 取变分我们有:
取变分我们有:
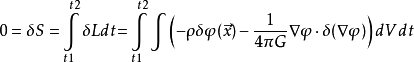
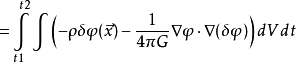
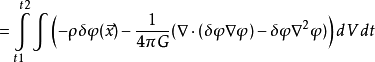
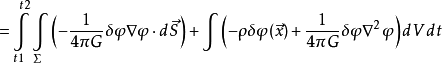
其中,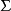 包围体积V的边界
包围体积V的边界
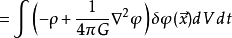
因此有引力场运动方程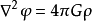 。 这样,我们有包含引力场和无压理想流体的总拉格朗日密度为:
。 这样,我们有包含引力场和无压理想流体的总拉格朗日密度为:
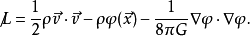 按照分析力学原理,我们有守恒量——哈密顿量(其中:
按照分析力学原理,我们有守恒量——哈密顿量(其中: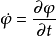 )为:
)为:
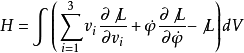
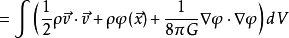 其中,
其中,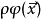 代表理想流体与引力场的相互作用能,可以将它归为理想流体的能量,也可以把它归为引力场的能量,我们现在把它归为引力场的能量,这时需要从引力场运动方程解出:
代表理想流体与引力场的相互作用能,可以将它归为理想流体的能量,也可以把它归为引力场的能量,我们现在把它归为引力场的能量,这时需要从引力场运动方程解出: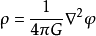 ,代入上式得:
,代入上式得:
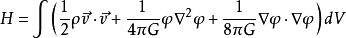
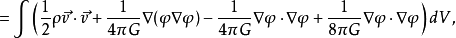
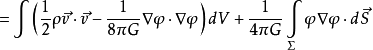 其中:
其中: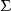 为包围体积V边界。体积V是全空间。 一般我们考虑有限区域的理想流体和引力场的情况,这时边界是无限远处,无限远处的边界条件是
为包围体积V边界。体积V是全空间。 一般我们考虑有限区域的理想流体和引力场的情况,这时边界是无限远处,无限远处的边界条件是 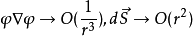 ,其积
,其积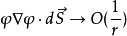 ,因此
,因此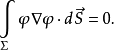 考虑到有限区域的理想流体和引力场以及边界条件,我们有:
考虑到有限区域的理想流体和引力场以及边界条件,我们有:
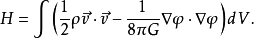
在分析力学中我们称哈密顿量为能量,因此又可写为:
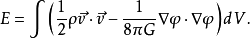
哈密顿量是守恒量,即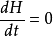 也即
也即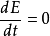 。 从上面的结果我们看到:
。 从上面的结果我们看到: 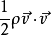 代表理想流体的动能密度
代表理想流体的动能密度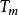 ,
,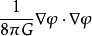 代表引力能密度
代表引力能密度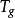 ,这时我们看到总能量密度是
,这时我们看到总能量密度是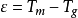 ,引力能贡献的是负能。当然,如果将相互作用能归为理想流体的能量,则引力能贡献的是正能,数值仍然是
,引力能贡献的是负能。当然,如果将相互作用能归为理想流体的能量,则引力能贡献的是正能,数值仍然是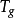 。
。
本词条内容贡献者为:
任毅如 - 副教授 - 湖南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国