[科普中国]-反响传播

反响传播指的是从最后一层反馈到第一层，并被用来计算误差相对于网络中每个单元权重的导数。

简介在实际操作中，这只是简单地将两个梯度数值相乘。反响传播从尾部开始，根据链式法则递归地向前计算梯度。

反响传播从从最上层的节点f开始，初始值为1，以层为单位进行处理。节点接受f发送的1并乘以该节点的偏导值-4等于-4，节点z接受f发送的1并乘以该节点的偏导值3等于3，至此第二层完毕，求出各节点总偏导值并继续向下一层发送。节点q向x发送-4并乘以偏导值1等于-4，节点q向y发送-4并乘以偏导值1等于-4，至此第三层完毕，节点x，y的偏导值都为-4，即顶点f对x,y的偏导数均为-4。1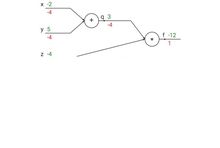

本质反响传播的本质只是对链式法则的巧妙运用。链式法则是在本科课程中导数的一个基本属性。它指出，假设有三个函数f、g和h，其中f是g的函数，g是h的函数，那么f相对于h的导数等于f相对于g的导数和g相对于h的导数的乘积。

原理我们使用最简单的神经网络来说明。这个网络只有3层，分别是蓝色的输入层、绿色的隐藏层和红色的输出层。上一层中的每个单元都连接到下一层中的每个单元，而且每个连接都具有一个权重，当某个单元向另一个单元传递信息时，会乘以该连接的权重得到更新信息。某个单元会把连接到它的上一层所有单元的输入值相加，并对这个总和执行Logistic函数并向下一层网络传递该值。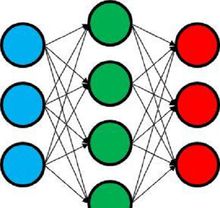

为了计算总误差，我们使用了训练集中的所有样本，并对红色输出层中的每个单元计算该单元预测值与真实输出间的平方误差。对每个样本分别计算并求和，得到总误差。

由于g为网络的预测值，取决于网络的权重，可以看到总误差会随权重变化而变化，网络的训练目标就是找到一组误差最小的权重。2

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学