在几何学中,阿波罗尼奥斯定理(Apollonius theorem)是一个关于三角形边长与中线长度关系的定理,它表示任何三角形的任意边的平方和等于第三边的一半的平方的两倍,加上第三边中位数的平方的两倍。
内容在几何形状中,阿波罗尼奥斯定理表示任何三角形的任意边的平方和等于第三边的一半的平方的两倍,加上第三边中位数的平方的两倍1。具体来说,在任何三角形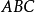 中,如果
中,如果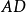 是中线,那么
是中线,那么
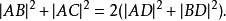
这是一个特殊情况的斯图尔特定理。对于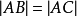 的等腰三角形,
的等腰三角形,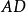 的中位线垂直于
的中位线垂直于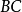 ,定理简化为三角形ADB(或三角形ADC)的毕达哥拉斯定理。从平行四边形的对角线相互平分的事实来看,该定理等价于平行四边形定律2。
,定理简化为三角形ADB(或三角形ADC)的毕达哥拉斯定理。从平行四边形的对角线相互平分的事实来看,该定理等价于平行四边形定律2。
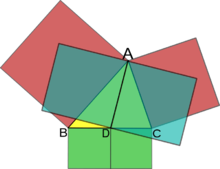
证明该定理可以证明是斯图尔特定理的一个特例,或者可以用向量证明。以下是使用余弦定律证明。
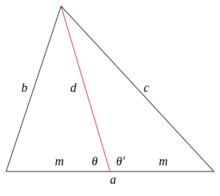
设三角形具有边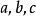 ,其中线
,其中线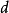 被绘制到a侧。设
被绘制到a侧。设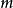 是由中线分割
是由中线分割 形成的线段长度,因此
形成的线段长度,因此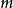 是
是 的一半。设
的一半。设 和
和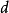 之间形成的角度为
之间形成的角度为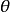 和
和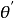 ,其中
,其中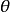 包括
包括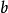 ,
,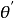 包括
包括 。那么
。那么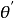 是
是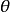 的补充,
的补充,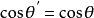 。由余弦定理可知:
。由余弦定理可知:
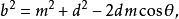
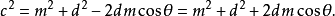
根据这些方程式可得,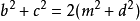 ,即得证。
,即得证。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国