[科普中国]-逆序法作图

有些作图题，需要在给定图形上作出具有某种性质的新图形，如果这样的新图形不易作出，那么可以首先在任意位置上按要求条件作出新图形，然后再把这个新图形移到给定图形上，并使移动后保持图形的合同性．这种作图方法称为逆序法或反求法1。

基本介绍逆序法作图(construction by reverse order)是与一般作图程序相反的一种作图方法，某些作图题，需要在给定图形上做出具体的符合某种性质的新图形，如果这样的图形不易作出，那么可以首先在任意位置上按要求条件作出新图形，然后再把这个新图形移到给定图形上，并使移动后保持图形的合同。

例如，在定圆中求作一直径，使它对圆内已知点所张开的角等于已知角，其思路要点是：如图，在⊙O内作一直径BC，使它对圆内已知点A所张开的角等于已知角α，相当于已知底边、顶角和底边的中线作三角形，但由于顶点A是固定的，底边是直径，所以这个三角形的位置在⊙O内无法确定，然而，如果在任意位置上作出这样的三角形，再将它移入⊙O内，是容易做到的，因此，本题采用逆序法作图为宜，由于A点在⊙O内，所以α>90°，否则无解；若α>90°，当AO>h(弓形弧 的高)时，△A′B′C′有两解；当AO=h时，△A′B′C′有一解，在将△A′B′C′移入⊙O时，由于AB一般有两解，因而符合条件的直径BC的解数比△A′B′C′的解数要加倍2。

例题解析【例1】在定角XOY的两边上各求一点A、B，使AB等于定长l，而O与AB的距离等于定长h (图3)。

分析：此问题实际上是要求在∠XOY上作一个三角形OAB，使它的一个角为∠XOY，对边AB=l，AB上的高为h。在∠XOY上直接作这样的三角形是非常困难的，因此，可采用逆序祛作图，在任意位置上作一个这样的三角形。然后再将这个三角形合同地移至∠XOY上。

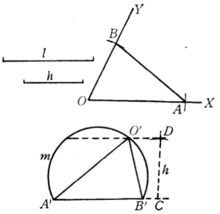
作法：作弓形弧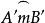 ，使弦A'B'=1，它所含的角等于∠XOY，作CD⊥A'B'，垂足为C，使CD=h。过D作A'B'的平行线交弓形弧于O'，连接A'O'、B'O'。

在∠XOY的边OX上，取OA=O'A'，在OY上， 取OB=O'B'，连接AB，则A、B为所求两点。

证明：根据作图，△AOB≌△A'O'B’，则A'B'=AB=l，因为A' B'上的高为h，所以O到AB的距离为h，所以，A、B为所求两点。

讨论：过D作A' B'的平行线与弓形弧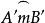的交点有三种情况： (i)有两个交点， 此时有两解；(ii) 有一个交点，此时有一解；(iii)无交点，此时无解1。

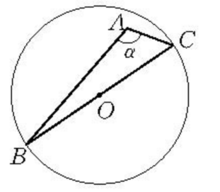
【例2】在定圆中求作一直径，使它对圆内已知点所张开的角等于已知角(图4)。

分析：假设直径BC合乎条件， 连接AB、AC (A为O0内已知点)，则∠BAC=a (已知角) .在△ABC中，BC、AO、∠BAC为已知，由此， 我们不难发现，在⊙O中作一直径使它对圆内已知点A所张开的角等于已知角，相当于已知底边、顶角和底边上的中线作三角形。但顶点A是固定的，底边又是直径(过圆心)，所以这个三角形的位置很难确定，然而，如果采用逆序法作图，即在任意位置上作出这样的三角形，再将它合同地移入⊙O内，是容易做到的。

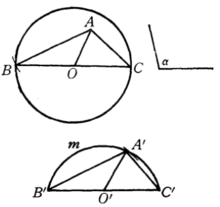
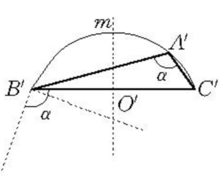
作法：作以⊙O的直径为弦，所含角等于α的弓形弧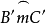，以B'C'的中点O'为圆心，以AO之长为半径画弧交弓形弧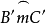于A'。连接A'B'、A'C'。

在⊙O内， 以A为圆心以A'B’为半径画弧交⊙O于B，连接BO并延长其交⊙O于C，BC即为所求直径。

证明：连接AB、BC、CA、AO。由作图△A'B'C'的底边为⊙O的直径，中线A'O'=AO，顶角A=a。

由作图知，△ABO≌△A'B'O' (三对对应边相等)。在△AOC与△A'O'C'中，AO= A'O'，OC=O'C'，

∵∠AOC=∠OBA+∠OAB， ∠A'O'C'=∠O'B'A'+∠O'A'B'，

∵∠AOC=∠A'O'C'，于是△AOC≌△A'O'C'，

从而△ABC≌△A'B'C'，所以BC为所求的直径。

讨论：由于A点在⊙O内，所以α>90°，否则本题无解。若αh (弓形弧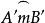的高)时，△A'B'C'有两解；当AO=h时，△A'B'C'有已解，当A0