[科普中国]-西姆森定理

西姆森定理（Simsson theorem），亦译为西姆松定理，是关于平面几何中的点共线的两个定理。表述为：过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线，则三垂足共线，此线常称为西姆松线或译西摩松线（Simson line）。西姆森定理的逆定理为：若一点在三角形三边所在直线上的射影共线，则该点在此三角形的外接圆上。

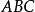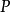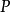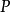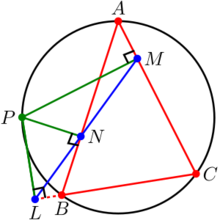
定理内容西姆松定理说明：有三角形 ，平面上有一点 。 在三角形三边上的投影（即由 到边上的垂足）共线（此线称为西姆松线或译西摩松线, Simson line）当且仅当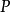 在三角形的外接圆上1。

相关的结果有：

（1）称三角形的垂心为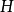 。西姆松线和 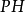的交点为线段 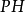的中点，且这点在九点圆上。

（2）两点的西姆松线的交角等于该两点的圆周角。

（3）若两个三角形的外接圆相同，这外接圆上的一点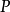 对应两者的西姆松线的交角，跟 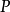的位置无关。

证明如图1，若L、M、N三点共线，连结BP，CP，则因PL垂直于BC，PM垂直于AC，PN垂直于AB，有B、P、L、N和M、P、L、C分别四点共圆，有∠PBN = ∠PLN = ∠PLM = ∠PCM，故A、B、P、C四点共圆。

若A、B、P、C四点共圆，则∠PBN = ∠PCM。因PL垂直于BC，PM垂直于AC，PN垂直于AB，有B、P、L、N和M、P、L、C四点共圆，有∠PLN = ∠PBN = ∠PCM =∠PLM，故L、M、N三点共线。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所