三维射影空间(three-dimensional projective space)常简称射影空间,射影几何研究的基本对象,指三维(空间)射影几何的全体点的集合。三维欧氏空间(或仿射空间)添加一个平面(即无穷远平面,它由所有直线上的无穷远点组成)后称为扩大空间,把扩大空间中的普通元素(点、直线和平面)和无穷远元素不加区别同等看待,这空间就成为射影空间的一个模型,反过来,若在一个射影空间中任意取定一个平面,把它当做无穷远平面,并把这平面上的点和直线当做无穷远点和无穷远直线,而将其余的点、直线和平面都当做有穷点、有穷直线和有穷平面,则该空间就可看做一个欧氏空间(或仿射空间)的扩大空间,即去掉了无穷远点后全体有穷点的集合是欧氏空间(仿射空间),射影空间具有与欧氏空间(仿射空间)不同的性质,例如在射影空间中,任何一个平面都不能把射影空间分成两部分,任何两个平面都相交,但它们却不能把射影空间分成四部分1。
基本介绍中心射影在平面上任取两条相交的直线a和a’(图1),并且在两条直线外任取—点S,在直线a上取一点A1,通过点S和点A1引直线SA1,设它与直线a'交于A'1,则点A'1叫做直线a上的点A1在a'上的中心射影,点S叫做射影中心,直线SA1叫做投射线2。

如果在直线a上取点A2,A3,……则用上述方法在直线a'上可以得到它们的射影A'2,A'3,……。
由点A1,A2,……求它们射影A'1,A'2,……的作法,叫做中心射影法。
从中心射影的定义,我们看出,如果A'1是直线a上点A1在直线a'上的射影,则A1也是直线a'上点A'1在直线a上的射影,一般来说对于直线a(或a’)上的一个点A(或A')总可以找到它在直线a'(或a)上的射影A'(或A)。但是我们看出,在欧几里得平面上使用中心射影法将遇到困难,这就是直线a上的点在直线a'上不一定都有射影,同时直线a'上的点也可能不是直线a上任何点的射影。换句话说就是点与它的射影之间不能作成一一对应。
例如,在直线a上取点An使投射线SAn平行于a',由于在欧几里得平面上平行线不相交,所以它在直线a'上没有射影。同样,如果在直线a'上取点A'm,使投射线SA'm平行于直线a,则它也不是直线a上任何点的射影。
因此,在欧几里得平面上利用中心射影法所建立的点之间的对应不是一对一的;如果不消除这个缺点,则应用中心射影法研究问题就有很大的障碍,因此,我们有必要对欧几里得平面进行某种改造,使改造后的平面,可以应用中心射影法建立点与它的射影之间的一一对应,而没有任何例外2。
无穷远元素的引入我们将要建立的射影变换,必须是元素间一一的对应,而且要把直线变成直线,这样才能包括仿射和正交变换,但是在欧氏平面上直线和直线之间在中心射影下不能建立点的一一对应,这就使我们遇到了很大的障碍,因此必须对欧氏平面进行拓广,使它成为一种新的平面,在这个平面上,利用中心射影法,能够使直线和直线间的点建立一一对应,究竟怎样对欧氏平面加以拓广呢?这就是引进无穷远元素.我们约定2:
约定1 所有的在同一方向上平行的直线族,相交于同一个点,这个点叫做无穷远点或理想点,用A∞、B∞等表示。
根据这一约定,在不同方向上的平行直线族必然交于不同的无穷远点,否则两组不同的平行线将成为在同一方向上平行的直线,这与已知矛盾。因为平面上的直线可有无穷多个方向,因此,平面上将有无穷多个无穷远点。
约定2 平面上所有无穷远点的集合组成一条直线,这条直线叫做无穷远直线,用a∞、b∞等表示。
无穷远直线实际是三维空间中平行平面的交线。
这样,我们就在每一个欧氏直线上添加了一个无穷远点,在每一个欧氏平面上添加了一条无穷远直线。
定义 增加了无穷远点的直线叫做射影直线,增加了无穷远直线的平面叫做射影平面。
我们还可以定义三维的射影空间。那就是增加第三个约定。
约定3 空间内一切无穷远点的集合组成一个平面,这个平面叫做无穷远平面。常用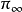 来表示。
来表示。
定义 增加了无穷远平面的空间叫做射影空间。
要注意,这两个定义里提到的新增加的无穷远元素与原来的元素(或叫有穷元素、
固有元素)的地位是完全相同,两者不应加以区分给以不同的对待,如果把无穷远点,直线或平面与原有的点,直线或平面加以区分,把无穷远元素看成是特定的元素来对待,这样的直线、平面和空间就是仿射的直线、平面或空间,这时把两条交于无穷远点的直线称为平行线,等等。
现在我们再回过头去看图1,由于引进了无穷远点,直线a上的An点将对应直线a'上的无穷远点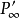 ,这是因为直线SAn平行于a';而直线a上的无穷远点
,这是因为直线SAn平行于a';而直线a上的无穷远点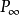 将对应直线a'上的A'm,这是因为a上的
将对应直线a'上的A'm,这是因为a上的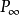 也是直线SA'm上的无穷远点,而
也是直线SA'm上的无穷远点,而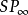 与a'交于A'm,这样,直线a与直线a'在以S为中心的中心射影下建立了点间的一一对应。不仅如此,这时以S为中心的线束与直线a上的点(或a'上的点)也建立了一一对应的关系,即直线SAi对应于点Ai,这两个对应是一维基本形间的一种透视对应,从这个对应关系中还看出,无穷远点可以与有穷远点互相对应。
与a'交于A'm,这样,直线a与直线a'在以S为中心的中心射影下建立了点间的一一对应。不仅如此,这时以S为中心的线束与直线a上的点(或a'上的点)也建立了一一对应的关系,即直线SAi对应于点Ai,这两个对应是一维基本形间的一种透视对应,从这个对应关系中还看出,无穷远点可以与有穷远点互相对应。
如果把无穷远元素特殊对待,以无穷远点为中心的中心射影就变成平行射影,这时所有投射线平行。
在推广了的平面上,“平行”与“相交”两个概念得到了统一,点和直线在结合关系上取得了对等的地位2。
空间中的射影坐标我们从扩充空间加以一般化,排除正常点与无穷远点的区分,即得出一般射影空间(或三维射影空间)概念。
在三维射影空间 中取不共面的四点
中取不共面的四点 以及不在这四点所决定的四面体的面上的任一点E,由这五点所构成的系统
以及不在这四点所决定的四面体的面上的任一点E,由这五点所构成的系统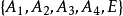 称为
称为 中的一个射影坐标系3。
中的一个射影坐标系3。
我们用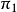 表示由点
表示由点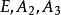 所决定的平面,用π2表示由点
所决定的平面,用π2表示由点 所决定的平面,而且用π3表示由点
所决定的平面,而且用π3表示由点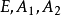 所决定的平面,这三个平面
所决定的平面,这三个平面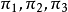 与
与 分别交于点
分别交于点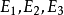 。
。
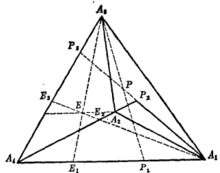
对射影空间 中任意一点P,用P1表示平面PA2A3与A4A1的交点,用P2表示平面PA1A3与A4A2的交点,用P3表示平面PA1A2与A4A3的交点。令
中任意一点P,用P1表示平面PA2A3与A4A1的交点,用P2表示平面PA1A3与A4A2的交点,用P3表示平面PA1A2与A4A3的交点。令
 则成比例的实数组
则成比例的实数组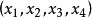 称为P点关于射影坐标系
称为P点关于射影坐标系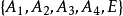 的射影坐标。
的射影坐标。
这时四面体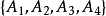 称为坐标四面体,E称为单位点;诸参考点的射影坐标分别为A1(1,0,0,0), A2(0,1,0, 0), A3(0, 0,1, 0),A4(0,0, 0,1), E(1,1,1, 1);四个坐标平面的方程分别为
称为坐标四面体,E称为单位点;诸参考点的射影坐标分别为A1(1,0,0,0), A2(0,1,0, 0), A3(0, 0,1, 0),A4(0,0, 0,1), E(1,1,1, 1);四个坐标平面的方程分别为 。
。
因此可把三维射影空间 看为点集,其点与不全为零的实数组
看为点集,其点与不全为零的实数组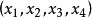 建立对应,并规定凡成比例的实数组
建立对应,并规定凡成比例的实数组 对立于同一点3。
对立于同一点3。
现在写出射影坐标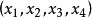 与齐次坐棕(x,y,z,t)之间的关系式,设坐标平面xi=0(i=1,2, 3,4)关于齐次坐标的方程
与齐次坐棕(x,y,z,t)之间的关系式,设坐标平面xi=0(i=1,2, 3,4)关于齐次坐标的方程
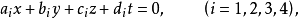 则有
则有
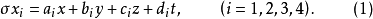 由于四个平面不共点,所以
由于四个平面不共点,所以

反之,假定已知四个不全内零的数之比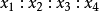 ,则解方程组(1),得出
,则解方程组(1),得出
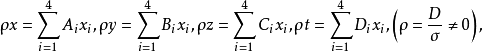 式中
式中 为
为 在行列式D中的代数余子式。这表示
在行列式D中的代数余子式。这表示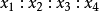 与
与 组成一个一一对立3。
组成一个一一对立3。
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国