[科普中国]-庞加莱复数平面模型

庞加莱复数平面模型(Poincaré complex plane model)是解释罗氏平面几何的模型。这个模型是庞加莱((J.-)H.Poincaré)首先提出来的，因为该模型的点是在复数上半平面上，所以称之为罗氏几何的庞加莱复数平面模型。庞加莱利用这个模型，在欧氏平面上解释了罗氏平面几何，若欧氏几何无矛盾，则罗氏几何亦无矛盾1。

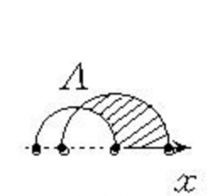
基本介绍庞加莱复数平面模型是解释罗氏平面几何的模型。取欧氏上半平面，其中的点称为罗氏点(不包括x轴上的点)，罗氏直线是指中心在x轴上不含有端点的半圆周以及上半平面中垂直于x轴的半直线(不含有x轴上的点，这样的半直线可以看成中心在x轴，半径为无限大的半圆周)，它们统称为欧氏半圆周或罗氏直线，端点为A，B的半圆弧表示罗氏线段AB.用起点在上半平面，终点在x轴上的弧OX表示罗氏半直线(X不是罗氏点)，罗氏角是指通过一点的两条罗氏半直线的集合1。

对应于欧氏点和半圆周，在罗氏点和罗氏直线之间建立如下的关系：

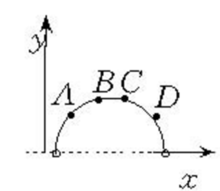
1.若点A在半圆周a上，则称罗氏点A在罗氏直线a上。

2.设A，B，C在半圆周a上，若B在A与C之间，则称罗氏直线a上的点B在A与C之间，即点在罗氏直线上的顺序与点在欧氏半圆周上的顺序相同。

3.这样的罗氏直线上存在戴德金原理。

4.在上半平面引进复数，使每一点M与一个复数x+iy之间建立对应，这样可以利用对半圆周的反演变换定义合同关系，即若经过几个反演变换的乘积把一个圆弧(角)变成另一个圆弧(角)，则称这两个罗氏线段(罗氏角)是合同的。

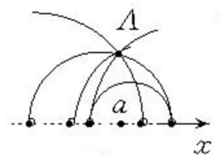
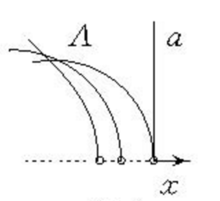
利用这些关系就可以证明这个模型满足罗氏平面几何的全部公理。例如，它满足罗氏几何的平行公理，若a是罗氏直线，A∉ a，过A可以引无数多条罗氏直线，与a没有公共点。即通过罗氏直线外的任意一点，可以引无数多条罗氏直线，与已知的直线共面而不相交1。

庞加莱简介庞加莱，法国人。1854年4月29日生于南锡市。他对数学深感兴趣，于1876年写出了论文《关于微分方程所定义的函数的性质》，于1878年发表在《高等工艺学校学报》上。同年，他写出了博士论文《自变量为任意个数的偏微分方程的积分》，获得了巴黎大学数学博士学位。1879年起庞加莱任卡恩大学教授。1881年起执教于巴黎大学。1908年被选为法国科学院院士。1912年7月17日在巴黎逝世2。

庞加莱是19世纪末20世纪初国家数学界的领袖人物，是一位对数学及其应用做了广泛的独创性、奠基性工作的大师。

首先，他创立了自守函数理论和微分方程定性理论。自守函数就是在某些变换群作用下不变的函数，它是圆函数、双曲函数、椭圆函数的推广。庞加莱深入研究了常微分方程所定义的积分曲线的形状和奇点的性质。他创立了研究微分方程的新方法，即不求解方程，而从方程本身出发，直接研究积分曲线的性质，就是解的性质。这个方法被称为微分方程的定性理论。

其次，庞加莱是组合拓扑学的奠基人。他研究了代数函数f(x，y，z)=0当x，y，z都是复数时的四维曲面的结构。值得一提的是，1912年他在逝世前不久得到了一个有重要价值的不动点理论：如果平切环的一个自身到自身的拓扑变换把它的一边(是圆周)沿着一个方向转动，而把另一边沿着相反的方向转动，同时保持面积不变，则在平切环里至少存在两个不动点。

第三，庞加莱在非欧几何、代数几何、偏微分方程、积分方程等领域里也作了许多贡献。如独立地得到了平面双曲几何的庞加莱模型；在代数几何中得到了一个普遍的单值化定理，并于1907年完成了这个定理的证明；1894年证明了偏微分方程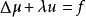(这里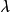是复数，在区域边界上u=0)在一个有界三维区域内的所有特征值的存在性及基本性质；等等。

庞加莱也是一位物理学家。

庞加菜同时还是一位自然科学哲学家，他主张数学的对象及真理不能脱离数学的真理或直觉而独立存在，它们应当能够通过理性的活动或直觉的活动而独立存在。发表了一系列的自然哲学名著2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所