[科普中国]-二阶曲线

二阶曲线(curve of order 2)是平面射影几何的基本研究对象。两射影线束对应直线的交点集称为二阶曲线。两个不共心、非透视的射影线束所成的二阶曲线称为常态二阶曲线。两个透视线束所成的二阶曲线称为变态的二阶曲线。由于二阶曲线和二级曲线从代数形式上看是一致的，都是二次方程，因此统称为二次曲线1。

基本介绍设在平面上点的齐次仿射坐标或射影坐标为(x1，x2，x3)，则满足三元二次齐次方程

的点的全体称为二阶曲线。这里aij为实数且至少有一个不是零，该方程称为这二阶曲线的方程，(aij)称为系数矩阵，若系数矩阵的行列式|aij|≠0，则二阶曲线称为非退化的，否则称其为退化的，退化的二阶曲线是两条直线(可以是虚直线)，在射影平面上，成射影对应的两个线束的对应直线的交点的集合是二阶曲线(参见本卷《平面解析几何》中的“二次曲线”)2。

二阶曲线的射影定义定理1 两个不共心的射影线束，其对应直线的交点集及该两个线束的中心组成一条二阶曲线。

定理1为二阶曲线提供了几何模型，是二阶曲线的存在定理。形成二阶曲线的两个射影线束的中心，由定理知，似乎与曲线上的其它点并不“平等”。但由下述定理可知，其实不然。

定理2 一条由两个射影线束的对应直线的交点构成的二阶曲线上，任意两点都可取作构成该曲线的两个射影线束的中心。

定理3 平面上任意无三点共线的五点可决定一条由两射影线束所成的二阶曲线。

定理4 任何二阶曲线都可由两个射影线束所成。

定义1 两射影线束对应直线的交点集称为二阶曲线。

特殊地，当射影对应是透视对应时，有：

两透视线束对应直线的交点如前讨论在透视轴上；且(图1)在两线束的公共直线SS'=t上的每一点，均是两透视线束S和S'中对应直线SS'∈S和S'S∈S‘的交点。因此，二阶曲线特殊地由两条直线组成：一是透视轴，一是两线束的公共线。

定义2两个不共心、非透视的射影线束所成的二阶曲线称为常态二阶曲线。两个透视线束所成的二阶曲线称为变态的二阶曲线。

由于二阶曲线和二级曲线从代数形式上看是一致的，都是二次方程，因此统称为二次曲线1。

二阶曲线上的射影变换二阶曲线上的射影变换(projective transformation on curves of order 2)是一种特殊的射影变换，若在二阶曲线的点之间建立了一一对应，使得二阶曲线上任意一点与各组对应点相连所构成的两个线束是射影对应的，则称在二阶曲线上建立了射影变换，二阶曲线称为底。如图，若O(A，B，C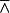，…)O(A′，B′，C′，…)，则A→A′，B→B′，C→C′，…决定射影变换，记为(A，B，C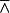，…)(A′，B′，C′，…)，也称它们为二阶曲线上的射影点列，射影变换与O点的取法无关，二阶曲线上的射影变换由三组对应点惟一决定，若给了二阶曲线上的一个射影变换，则对于任意两组对应点M，M′与N，N′，直线MN′与M′N的交点总在一条确定的直线上，这条直线就是已知变换的透视轴2。

二阶曲线的极点二阶曲线的极点(pole of curve of order 2)射影几何的基本概念之一.给定一个非退化的二阶曲线Γ和不在Γ上的点P，过P作直线交Γ于M1，M2，若Q是直线PM1上一点，且(M1M2，PQ)=-1，则称P与Q关于二阶曲线Γ调和共轭或关于Γ互为共轭点，点P关于二阶曲线Γ的调和共轭点的轨迹是一条直线，称为点P的极线，点P称为这直线的极点。若点P在二阶曲线上，则规定其极线就是它的切线。反之，切线的极点就是它的切点。这样，对于非退化的二阶曲线，极点和它的极线之间就建立了一一对应的关系。如果二阶曲线为2

则点p(p1，p2，p3)的极线方程是

反之，直线l[u1，u2，u3]的极点P(p1，p2，p3)的坐标可由下列方程组解出

二阶曲线的奇异点二阶曲线的奇异点(singular point of curve of order 2)是二阶曲线上的特殊点，简称奇点。即二阶曲线（1）上满足条件

的点P(p1，p2，p3)，二阶曲线非退化的充分必要条件是无奇异点，退化二阶曲线必有奇异点(可以是虚点)，且当系数矩阵(aij)的秩等于2时，有惟一奇异点;当(aij)的秩等于1时，有无穷多个奇异点，它们在同一条直线上。二阶曲线的奇异点有简单的几何意义：二阶曲线上一点是奇异点的充分必要条件是它与曲线上任何点的连线含于此曲线上2。

二阶曲线上的对合二阶曲线上的对合(involution on a curve of order 2)是指二阶曲线上的一种特殊射影变换，若在二阶曲线上的点之间建立了非恒等的一一对应，以曲线上任一点为中心与曲线上对应点的连线构成两个线束，如果这两个线束是对合的，则称在二阶曲线上所建立的对应是对合，二阶曲线上的对合由两对对应点惟一确定2。

二阶曲线的射影分类二阶曲线的射影分类(projective classification of curve of order 2)是二阶曲线的一种分类方法，指用射影等价关系对二阶曲线进行的分类。射影平面上的二阶曲线（1）的集合在射影群之下分为五个射影类，其标准方程和曲线名称分别为：

1.， 非退化的实二阶曲线。

2.， 非退化的虚二阶曲线。

3.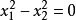，一对实直线。

4.，一对虚直线。

5.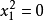，一对重合直线。

在同一类里的任意两条二阶曲线射影等价，即存在某一射影变换，将其中一条曲线变为另一条曲线。而不同类中的任意两条曲线不射影等价2。

二阶曲线的内接n点形二阶曲线的内接n点形(inscribed n-gon of curve of order 2)是指顶点都在一个非退化二阶曲线上的n点形，若一个n点形(简单的或完全的)的顶点都在一个非退化二阶曲线上，则这个n点形称为该二阶曲线的内接n点形(简单的或完全的)2。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学