[科普中国]-同素射影对应

同素射影对应是一种特殊的射影对应，即同类基本形间的射影对应。例如，把点变成点，或直线变成直线的射影对应都称为同素射影对应。

基本介绍同类基本形间的射影对应叫做同素射影对应，同素射影对应是一种特殊的射影对应，例如，把点变成点，或直线变成直线的射影对应都称为同素射影对应。

相关介绍射影对应是射影几何中最重要的一种对应，通常指射影空间(平面、直线)之间保持共线性和共线四点的交比不变的点的一一对应。在两个射影空间(平面、直线)都建立了射影坐标系后，它们之间的射影对应可以用对应点坐标之间的关系表出。例如，对于两个射影平面π与π′，若平面π上点P的射影坐标为x1，x2，x3，其对应的π′上点P′的射影坐标为x′1，x′2，x′3，则射影对应有代数表达式

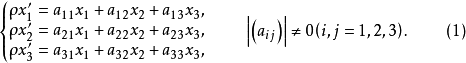其中ρ≠0是齐次坐标的比例常数，|(aij)|是矩阵(aij)的行列式。因此，也可以直接用点的射影坐标之间的齐次非奇异线性变换(1)来定义射影对应。当两个对应的射影空间(平面、直线)重合时，这种集合到自身的射影对应，通常称为射影空间(平面、直线)的射影变换.在射影空间(平面、直线)中建立射影坐标系后，射影变换可以用对应点的坐标之间的关系表出。例如，在射影平面上把具有射影坐标x1，x2，x3的点变成具有射影坐标x′1，x′2，x′3的点的射影变换同样有代数表达式(1)。因此，同样可以直接用点的坐标的齐次非奇异线性变换(1)来定义射影变换1。

二维变换指点场到点场，线场到线场的变换，点场和线场是二维基本形，平面上所有点的集合叫点场，平面上所有直线的集合叫线场。

非奇线性对应必是平面π上与平面π'上点之间的一一对应，平面π上的点到平面π'上的点的非奇性对应建立了π上的直线到π'上的直线的非奇线性对应。也就是点场到点场的非奇线性对应必建立线场到线场的非奇线性对应。射影对应也可以定义为满足共线点的象仍是共线点，且任何共线四点的交比等于对应四点的交比的一一对应。同样可以定义线场到线场之间的射影对应定义。

两平面的点之间的透视对应必是射影对应；点场到点场或线场到线场的射影对应叫同素射影对应，因点场与线场是对偶图形，四对对应元素(如四对对应点，每三点不共线)可确定非奇线性对应，即有四个独立条件，再给定一点P，则可唯一确定其对应点P'，若Pi(i=1,2,3,4)四点中无三者共线,那么使这四点不变的射影变换一定是恒等变换，即非恒等的射影变换不能有四个不变点2。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所