[科普中国]-中心仿射变换

中心仿射变换(central affine transformation)是一类重要的仿射变换，指含一个不变点的仿射变换。位似变换是中心仿射变换的特例。

定义中心仿射变换是指含一个不变点的仿射变换，这个不变点称为中心仿射变换的中心。在以变换中心为坐标原点的仿射坐标系中，中心仿射变换公式右端的常数项为0。例如，在平面仿射坐标系中，变换

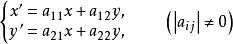是一个中心仿射变换，其变换中心为坐标原点1。

在平面和空间的变换下，可以有—些点或图形的象就是它们自己，这就是说它俩并不被变换所改变，因此我们把这种点或图形叫做已知变换的不变的点或图形。有一个不变点的仿射变换叫做中心仿射变换，不变点就叫做变换的中心。假如取一个中心仿射变换的中心作为坐标原点，则变换公式左边就没有了自由项。因此我们知道，以坐标原点作为中心的中心仿射变换的公式是

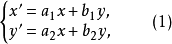或

变换公式(1)或(2)右边是齐次的，在代数上叫做齐次线性变换。因此，以坐标原点作为中心的中心仿射变换的公式是行列式不等于零的齐次线性变换。反之，行列式不等于零的齐次线性变换总表示中心仿射变换(我们还知道它同时可以表示坐标原点不变的仿射坐标变换)。

正像仿射坐标变换可以分移轴和坐标原点不变的坐标变换两步来完成—样，一般的仿射变换也可以分平移和中心仿射变换两步来完成。这两个几何事突不过是同一个代数事实的不同的解释罢了，从代数上说则是：一般的线性变换都可以分移轴(我们借用这个名词)和齐次线性变换两步来完成2。

中心仿射群仿射几何是由线性变换群

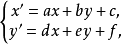制约的。这种变换可以认为是

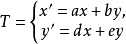和平移

复合而成的。上面像T的这种变换称为齐次仿射变换或中心仿****射变换，这种变换构成的集称为齐次仿射群或中心仿射群。用“中心的"这个形容词是因为原点或“中心”在这种变换下不变(用x=0，y=0代入即得)。式中a,b,d,e是实参数，并且满足ae-bd≠0。加上这个条件的原因是：由T的变换公式可以从x和y算出x'和y'，但在ae-bd=0时，这并非克莱因

的变换。当ae-bd≠0时，读者用中学代数中解二元一次方程组的办法可从T的变换式由x'和y'算出x和y。因而这时T是个变换(一对一的到上映照)。注意，旋转是一种特殊的仿射变换，此时a=e=cosθ，b=sinθ，d=-sinθ，而ae-bd=cos2θ+sin2θ=13。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所