[科普中国]-哈密顿力学-

哈密顿力学是哈密顿于1833年建立的经典力学的重新表述，它由拉格朗日力学演变而来。拉格朗日力学是经典力学的另一表述，由拉格朗日于1788年建立。哈密顿力学与拉格朗日力学不同的是前者可以使用辛空间而不依赖于拉格朗日力学表述。1

适合用哈密顿力学表述的动力系统称为哈密顿系统。

数学表述任何辛流形上的光滑实值函数H可以用来定义一个哈密顿系统。函数H称为哈密顿量或者能量函数。该辛流形则称为相空间。哈密顿量在辛流形上导出一个特殊的矢量场，称为辛矢量场。2

该辛矢量场，称为哈密顿矢量场，导出一个流形上的哈密顿流。该矢量场的一个积分曲线是一个流形的变换的单参数族；该曲线的参数通常称为时间。该时间的演变由辛同胚给出。根据刘维尔定理每个辛同胚保持相空间的体积形式不变。由哈密顿流导出的辛同胚的族通常称为哈密顿系统的哈密顿力学。

哈密顿矢量场也导出一个特殊的操作，泊松括号。泊松括号作用于辛流形上的函数，给了流形上的函数空间一个李代数的结构。特别的有，给定一个函数f

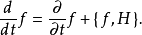
若我们有一个概率分布ρ，则（因为相空间速度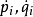（）有0散度，而概率是不变的）其传达导数（convective derivative）可以证明为0，所以

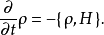这称为刘维尔定理。每个辛流形上的光滑函数G产生一个单参数辛同胚族，而若{G,H} = 0,则G是守恒的，而该辛同胚是对称变换。

哈密顿矢量场的可积性是未解决的问题。通常，哈密顿系统是混沌的；测度，完备性，可积性和稳定性的概念没有良好的定义。迄今为止，动力系统的研究主要是定性的，而非定量的科学。

哈密顿系统的几何哈密顿系统可以理解为时间R上的一个纤维丛E，其纤维Et，t∈R是位置空间。拉格朗日量则是E上的jet丛（射流丛）J上的函数；取拉格朗日量的纤维内的勒让德变换就产生了一个时间上的对偶丛的函数，其在t的纤维是余切空间TEt，它有一个自然的辛形式，而这个函数就是哈密顿量。

黎曼流形哈密顿量的重要特例是二次型，也就是，可以如下表达的哈密顿量

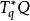
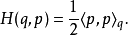其中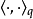是纤维（组态空间中的点q上的余切空间）上的余度量。该哈密顿量完全由动能项组成。

若考虑一个黎曼流形或一个伪黎曼流形，使得存在一个可逆，非退化的度量，则该余度量可以简单的由该度量的逆给出。哈密顿-雅可比方程的解就是流形上的测地线。特别的有，这个情况下的哈密顿流就是测地流。这些解的存在性和解集的完备性在测地线条目中有详细讨论。

亚黎曼流形当余度量是退化的时，它不是可逆的。在这个情况下，这不是一个黎曼流形，因为它没有一个度量。但是，哈密顿量依然存在。这个情况下，在流形Q的每一点q余度量是退化的，因此余度量的阶小于流行Q的维度，因而是一个亚黎曼流形。

这种情况下的哈密顿量称为亚黎曼哈密顿量。每个这样的哈密顿量唯一的决定余度量，反过来也是一样。这意味着每个亚黎曼流形由其亚黎曼哈密顿量唯一的决定，而其逆命题也为真：每个亚黎曼流形有唯一的亚黎曼哈密顿量。亚黎曼测地线的存在性由周-腊雪夫斯基定理给出。

连续实值海森堡群提供了亚黎曼流形的一个例子。对于海森堡群，哈密顿量为

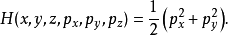
泊松代数哈密尔顿系统可以几种方式推广。如果不仅简单的利用辛流形上的光滑函数的结合代数，哈密尔顿系统可以用更一般的交换有单位的实泊松代数表述。一个状态是一个（装备了恰当的拓扑结构的）泊松代数上的连续线性泛函，使得对于代数中的每个元素A，A映射到非负实数。