[科普中国]-射影角度

射影角度(projective angular measure)是射影几何的一个术语，指射影几何中所定义的两条直线的夹角。例如，在射影平面上取定一个非退化的二级曲线，另选定一个常数k(k≠0)，从这个平面上任意两直线a，b的交点作这个二级曲线的切线p，q，则w(a，b)=kln(ab，pq)是两直线a，b的函数，且有以下性质：对于任何共点直线a，b，c，均满足w(a，b)+w(b，c)=w(a，c)，由于函数w(a，b)由有序两直线a，b惟一决定，并且满足射影不变性和可加性，因此把函数w(a，b)称为两直线a，b所成角(或夹角)的射影测度，简称两直线a，b的射影角度。射影角度是射影变换下的不变量，预先取定的非退化的二级曲线称为这测度的绝对形，k称为测度系数或单位1。

基本介绍距离的射影测度(射影距离)和夹角的射影测度(射影角度)合称为射影测度(projective measure)。射影测度是凯莱(A.Cayley)于1859年建立的，1871年，克莱因(C.F.Klein)利用射影测度的概念来说明非欧几何学。非退化的二阶曲线有实虚两种情况，若绝对形为非退化的实二阶曲线，则可构成罗氏几何；若绝对形为非退化的虚二阶曲线，则可构成黎氏几何，这两种几何合称非欧几何，这样非欧几何就可以从射影测度的概念导出，因为射影测度是由交比来定义的，它属于射影性质，所以非欧几何可以利用射影测度从射影几何导出1。

在平面内，取定一条常态二级曲线，并选定一常数k(k≠0)。对于平面内的任意两条直线a、b，从它们的交点引的两条切线t1、t2(图1)，作函数

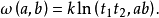因为二直线a、b确定以后，它们的交点也就唯一地确定，二切线t1、t2随即也被确定，由于

所以函数由二直线a、b唯一确定(除符号外)。利用交比的性质，可以验证函数满足下列三个条件2：

1．，

2．；

3．若直线a、b、c相交于一点，则

定义函数称为二直线a、b的有向夹角的射影测度，简称为射影角度。预先规定的二级曲线称为这测度的绝对形，常数k称为测度系数2。

下面我们研究射影角度的表达式。

设二级曲线(给定的绝对形)的方程为

二直线a、b的坐标分别为及，由a、b的交点所引的二切线t1、t2(它们a、b属于同一线束)的坐标可以表为

由于与二级曲线相切，故有

展开，得

其中。

所以

如果以表示这两个根，那么的坐标分别为

因此

关于射影角度，我们有如下的定理。

定理如果二直线的交点在绝对形上，则它们的夹角的射影测度等于零。

证明若二直线a、b的交点在绝对形上，过此交点所引的的两条切线重合为一条直线，即，交比(tt，ab)=1。

。

定理说明，两条平行直线所成的夹角等于零2。

相关概念在平面内，给定一条常态的二阶曲级 ，并选定一常数K(K≠0)。对于平面内的任意两点A、B，它们的连线交二阶曲线 于P1、P2(图2)，作函数

函数d(A，B)被A、B两点唯一确定(除符号外)，利用交比的性质，可以验证函数d(A，B)满足下列三个条件；

1．d(A，A)=0；

2．d(A，B)=-d(B，A)；

3．若A、B、C是一直线上的三点，则d(A，B)+d(B，C)=d(A，C)。

定义函数 称为两点A、B间的有向距离的射影测度，简称为射影距离。预先规定的二阶曲线称为这测度的绝对形，常数K称为测度系数2。

设二阶曲线的方程为

二点A，B的坐标分别为(a1，a2，a3)及(b1，b2，b3)，类似地可求出射影距离的表达式

其中 。

由射影距离的定义还可以看出，当A(或B) P1(或P2)时，交比(P1P2，AB) 0，d(A，B) 。因此有

定理平面上任何一点与绝对形上的任何点间的射影距离为无穷大。

由定理可以看出，作为绝对形的二阶曲线 与欧氏测度中的无限远直线 相当。

定义设二直线的交点在实的绝对形上，则称这二直线为平行直线2。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学