[科普中国]-螺线矢量场

在矢量分析中，一螺线矢量场（solenoidal vector field）是一种矢量场v，其散度为零。

性质在矢量分析中，一螺线矢量场1（solenoidal vector field）是一种矢量场v，其散度为零：

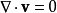
此条件被满足的情形是若当v具有一矢势A，即

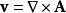
成立时，则原来提及的关系

会自动成立。

逻辑上的反向关系亦成立：任何螺线矢量场v，皆存在有一矢势A，使得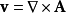。（严格来说，此关系要成立，受限到一些关于v的技术性条件，参见亥姆霍兹分解（Helmholtz decomposition））

散度定理能够针对螺线场给出等价的积分形式定义，亦即：任何闭曲面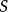，通过曲面的净通量会是零：

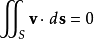
其中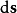是法矢量朝外的面元。

词源学螺线矢量场起源于希腊语中的螺线管，它是σωληνοειδές（sōlēnoeidēs），意思是管形或者管道。在螺线管的当前环境中，它意味着像在管道中一样受约束，因此具有固定的体积。

例子磁场B是螺线矢量场（参见麦克斯韦方程组）；

不可压缩流体的速度场是螺线矢量场。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所