热动力势能(英语:Thermodynamic potential)是一个来表示系统之热动力态的标量函数。热动力势能的概念是皮埃尔·迪昂于1886年提出。约西亚·吉布斯在他的论文中使用了基础函数一词。热动力势能其中一种主要的物理解释是内能U。它是守恒力系统之位形的能量(这就是为什么它是一个势能),只有在一套被定义出来的参考系中才具有意义。所有的热动力势能表示式可从U的表示式经勒让德变换导出。在热动力学中,某些力,如重力通常在势能的表示式中被忽略。例如:在所有的蒸汽引擎中,工作流体在山上的重力势能比在平地上的重力势能更高,重力势能项在内能的方程中通常会被省略,因为引擎的运作过程中,重力势能的改变量是可以忽略的。
描述与解释
|| ||
T为温度,S为熵,p为压力,V为体积。荷目霍兹自由能通常以F表示,但是国际纯粹与应用化学联合会采用A来作为符号。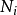 是系统里i型的粒子数,
是系统里i型的粒子数,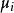 是i型粒子的化学势。为了保持完整性,
是i型粒子的化学势。为了保持完整性,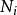 集合也包含了自然变量,虽然他们有时会被忽略。
集合也包含了自然变量,虽然他们有时会被忽略。
这五种常见的位都是能量位(在英语中potential与potential energy有时会混用),不过他们也是熵位。热动力方型图可以用来找出你想要的势能。
就像在机械力学中势能被定义为作功的能力,不同的势能有不同的意义。内能是作功的能力加上放热的能力。吉布斯能是作非机械功的能力。焓是作非机械功的能力加上放热的能力。亥姆霍兹自由能是作机械功加上非机械功的能力。从这些定义我们可以说ΔU是加到系统里的能量,ΔF是对系统作的总功,ΔG是对系统作的非机械功,ΔH是对系统作的非机械功加上给系统的热。当要计算化学反应的平衡结果与测量化学反应时材料的性质时,热动力位是非常有用的。化学反应通常在一些限制里发生,如定压、定温、定熵或定体积,这些条件成立时,有相应的热动力势能可以用来操作。如同机械力学,系统会趋向较低的势能值并达成平衡。根据这些限制,势能会达到一个不再变动的最小值。热动力势能可以用来估计在相应的限制中,热动力系统中可用的总能量。
特例:
1)当一个封闭系统的熵与“外部参数”(如:体积)保持定值,在平衡时内能(U)会降低并达到最小值。这根据热动力学第一与第二定律,也叫作最小能量原理,以下三行也是从此原理导出。
2)当一个封闭系统的温度与外部参数保持定值,在平衡时荷姆霍兹自由能(F)会降低并达到最小值。
3)当一个封闭系统的压力与外部参数保持定值,在平衡时焓(H)会降低并达到最小值。
4)当一个封闭系统的温度、压力与外部参数保持定值,在平衡时吉布斯能(G)会降低并达到最小值。
基础方程热动力势能的定义可能和热动力学第一与第二定律有所差别,这组微分方程之前叫作基础方程。1根据热动力学第一定律,任何系统内能U的微分变量可以写成进入系统的热与系统对环境作的功与任何加入系统的新粒子的和。
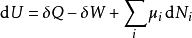 这里的
这里的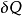 是流入系统的无限小的热,
是流入系统的无限小的热,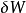 是系统作的无限小的功
是系统作的无限小的功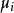 是i粒子的化学位,
是i粒子的化学位,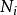 是i粒子的粒子数。(注意:
是i粒子的粒子数。(注意: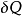 与
与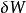 都不是恰当微分。所以这些变量的微小变化在此记为δ而不是d。)
都不是恰当微分。所以这些变量的微小变化在此记为δ而不是d。)
根据热动力学第二定律,我们可以由状态函数与它们的微分来表示内能的改变。如果发生在准静态变化中,我们得到:
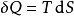
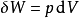 这里T是温度,S是熵,p是压力,V是体积。当是可逆过程时等号成立。
这里T是温度,S是熵,p是压力,V是体积。当是可逆过程时等号成立。
这领出了内能在准静可逆变化中的标准微分形式:
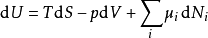 由于U、S、V是状态的热动力函数,上述关系在任意非可逆变化中也成立。如果系统拥有更多的外部变量而不是只有体积可以改变,基础热动力关系即可推广到:
由于U、S、V是状态的热动力函数,上述关系在任意非可逆变化中也成立。如果系统拥有更多的外部变量而不是只有体积可以改变,基础热动力关系即可推广到:
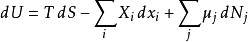
这里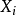 是对应到外部变量
是对应到外部变量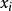 的广义力。
的广义力。
多应用几次勒让德转换,下列这四项势能的微分关系也成立:
|| ||
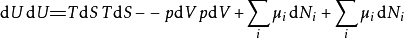
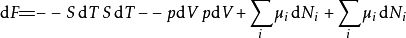
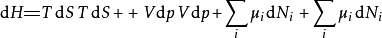
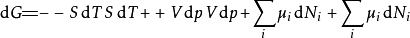 注意上述每个等式右边的无限小的量皆是等式左方的势能的自然变量。类似的方程如系统的所有其他热动力势能可以被找出。这里将有一个基础方程为每个热动力势能造成总计为
注意上述每个等式右边的无限小的量皆是等式左方的势能的自然变量。类似的方程如系统的所有其他热动力势能可以被找出。这里将有一个基础方程为每个热动力势能造成总计为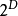 个基础方程。
个基础方程。
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国