[科普中国]-维度减化

维度减化（英语：Dimensional reduction）是紧化理论中紧致化的维度的大小变为零时的临界情况。在物理学中，通过将所有的场独立存在于额外维度D中，时空维数D的理论能够被较少数量的额外维度D重新定义。

维度减化详解例如，考虑一个周期性的紧凑的维度的L时期。让x成为沿着这条维度的坐标。任何场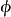 可以被描述为以下单元的总和：

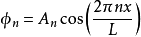
An作为一个常数。根据量子力学，这一单元具有沿着x轴的动量nh/L，在那里h是普朗克常数。因此，当L达到0时，这个动量达到了无限大，能量也一样，除非n=0。然而n=0提供了一个关于x恒定的场。因此在这个场的限制下，并在有限的能量下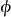， 将不依赖于x。

这种说法进行了概括。紧凑的维度对所有场施加了特定的边界条件，例如在周期性维度的情况下的周期性边界条件，并且在其他情况下通常为诺伊曼边界条件或狄利克雷边界条件。1现在假设紧凑的维度的尺度是L；那么沿这个维度的梯度的可能的特征值是1/L的整数或半整数倍（取决于精确的边界条件）。在量子力学中，这个特征值是场的动量，因此与其能量有关。当L→0时，除零之外的所有特征值都到无穷大，而能量也是如此。因此，在这个极限情况下，在有限能量的情况下，零是唯一可能的沿着紧凑尺寸的梯度下的特征值，这意味着没有任何东西依赖于这个维度。

背景将五维时空分开成四维的爱因斯坦方程式以及麦克斯韦方程组是首先由古纳尔·诺德斯特诺姆于1914年所发现，出现在他的重力理论内文中，但随后就被世人遗忘。在1926年，奥斯卡·克莱因（Oskar Klein）提议了第四个空间维度卷曲成一个半径非常小的圆，所以粒子沿着这个轴移动很短的距离，就会回到起始点。粒子在回到起始点前所能行进的距离则称作是该维度的大小。这个额外维度（extra dimension）是一个紧集，而时空具有紧致维度的现象则称作是紧化。

第五维度卷曲成圆，构成了最早的高维宇宙模型。此模型仅多出现了一个额外维度。

现代几何学中，额外的第五维度可以被理解为圆群U(1)，而基本上，电磁学可以用在纤维丛上规范群U（1）的规范场论来诠释。一旦这样的几何诠释能被理解，则将U（1）换成广义的李群就显得容易而直观。这样的推广常称作是杨-米尔斯理论。若要提到两者的差异，则可说杨–米尔斯理论是在平坦时空的场合处理，而卡鲁扎-克莱因理论则是在更具一般性的弯曲时空中处理。卡鲁扎-克莱因理论的底空间不一定是四维时空，而可以是任何的（伪）黎曼流形，或者甚至是超对称流形、轨形或非交换空间。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所