[科普中国]-判定边界

在具有两个类的统计分类问题中，判定边界或判定表面是超曲面，其将基础向量空间划分为两个集合，每个集合一个集合。 分类器将决策边界一侧的所有点分类为属于一个类，而将另一侧的所有点分类为属于另一个类。

介绍判定边界是问题空间的区域，分类器的输出标签是模糊的。如果判定表面是超平面，那么分类问题是线性的，并且类是线性可分的。

判定界限并不总是明确的。 也就是说，从特征空间中的一个类到另一个类的过渡不是不连续的，而是渐变的。 这种效应在基于模糊逻辑的分类算法中很常见，其中一类或另一类的成员资格不明确。

如：我们可以绘制出来x1+x2=3，这条线便是我们模型的分界线，也称之为判定边界。

神经网络和支持向量模型在基于反向传播的人工神经网络或感知器的情况下，网络可以学习的判定边界的类型取决于网络所具有的隐藏层的数量。如果它没有隐藏层，那么它只能学习线性问题。如果它有一个隐含层，那么它可以学习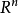的紧子集上的任意连续函数，如通用逼近定理所示，因此它可以具有任意的判定边界1。

具体来说，支持向量机找到一个超平面，它将特征空间分为两个具有最大余量的类。如果问题最初不是线性可分的，则通过增加维数来使用内核技巧将其转换为线性可分的问题。因此，小尺寸空间中的一般超曲面在具有更大尺寸的空间中变成超平面。

神经网络试图学习决策边界，最小化经验误差，而支持向量机试图学习决策边界，最大化判定边界和数据点之间的经验边际。

本词条内容贡献者为:

王慧维 - 副研究员 - 西南大学