[科普中国]-系统F

系统F，也叫做多态lambda演算或二阶lambda演算，是有类型lambda演算。它由逻辑学家Jean-Yves Girard和计算机科学家John C. Reynolds独立发现的。系统F形式化了编程语言中的参数多态的概念。

简介正如同lambda演算有取值于（rang over）函数的变量，和来自它们的粘合子（binder）；二阶lambda演算取值自类型，和来自它们的粘合子。

作为一个例子，恒等函数有形如A→ A的任何类型的事实可以在系统F中被形式化为如下式判断：

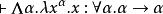
这里的α是类型变量。

在Curry-Howard同构下，系统F对应于二阶逻辑。

系统F，和甚至更加有表达力的lambda演算一起，可被看作Lambda立方体的一部分。1

逻辑和谓词布尔类型被定义为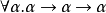： ，这里的α是类型变量。这产生了下列对布尔值TRUE和FALSE的两个定义，如下式：

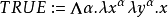
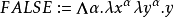
接着，通过这两个λ-项，我们可以定义一些逻辑算子：

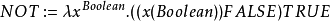
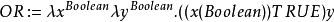
实际上不需要IFTHENELSE函数，因为你可以只使用原始布尔类型的项作为判定（decision）函数。但是如果需要一个的话：

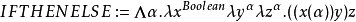
谓词是返回布尔值的函数。最基本的谓词是ISZERO，它返回TRUE当且仅当它的参数是邱奇数0：

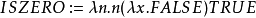
系统F结构系统F允许以同Martin-Löf类型论有关的自然的方式嵌入递归构造。抽象结构（S）是使用构造子建立的。有函数被定类型为：

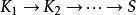
当S自身出现类型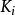 中的一个内的时候递归就出现了。如果你有m个这种构造子，你可以定义S为：

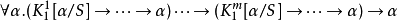
例如，自然数可以被定义为使用构造子的归纳数据类型N

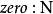
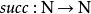
对应于这个结构的系统F类型是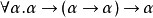 。这个类型的项由有类型版本的邱奇数构成，前几个是：

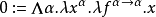
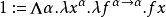
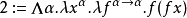
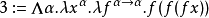
如果我们反转curried参数的次序（比如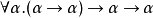 ），则n的邱奇数是接受函数f作为参数并返回f的n次幂的函数。就是说，邱奇数是一个高阶函数-- 它接受一个单一参数函数f，并返回另一个单一参数函数。2

用在编程语言中本文用的系统F版本是显式类型的，或邱奇风格的演算。包含在λ-项内的类型信息使类型检查直接了当。JoeWells（1994）设立了一个"难为人的公开问题"，证明系统 F的Curry-风格的变体是不可判定的，它缺乏明显的类型提示。

Wells的结果暗含着系统F的类型推论是不可能的。一个限制版本的系统F叫做"Hindley-Milner"，或简称"HM"，有一个容易的类型推论算法，并用于了很多强类型的函数式编程语言，比如Haskell和ML。2

本词条内容贡献者为:

王慧维 - 副研究员 - 西南大学