[科普中国]-不完全微分

不完全微分是实际微分作用与理想微分作用(应与偏差的变化速率成正比)间存在一定差距，等价于在理想微分环节后串接一个阻容环节的输出。

背景随着科学技术的不断进步和发展，被控对象正变得越来越复杂,，多年以来其改进算法层出不穷，如不完全微分的PID 算法。而人们对其控制精度的要求却日益提高，此时常规调节器不可能得到好的控制品质，基于以往工程方法来整定PID 参数已经不能满足控制要求了，这样就产生了复杂性和精确性的尖锐矛盾。智能自适应控制是解决上述问题的有效方法之一，其中神经网络以其良好的自适应自学习能力，使得它可以作为一种很好的方法而得以应用1。使用神经网络实现直接或间接的PID 控制，经过证实是有效的，它实现了PID 的自适应控制，使得传统的PID控制得以能够继续发挥其在控制中的良好作用。然而,，一般神经网络实现的PID 控制基本上都是使用一般的PID 控制算法， 而并未使用不完全微分PID 控制算法。在本文中, 将不完全微分PID 算法与神经网络相结合，组成基于不完全微分PID 算法的神经网络控制器， 共同发挥二者的优势，通过仿真实验可以看出该控制器提高了控制效果1。

定义形式一：将低通滤波器直接加在微分环节上2。

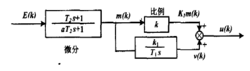
其中传递函数为：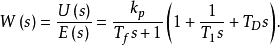

形式二：将低通滤波器加载整个系统后。

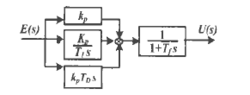
其中传递函数为：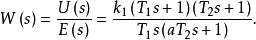

应用不完全的微分它使得在偏差作阶跃式变化时出现的输出瞬时跳变得到一定程度的缓和，因而在实际的PID控制算法中得到广泛采用。在PID 控制中，微分信号的引入可以改善系统的动态特性，但也易引入高频干扰，在误差扰动突变的时候尤其显出微分项的不足。要想解决这个问题，可以在控制算法中加入低通滤波器，方法之一就是在PID算法中加入一个一阶惯性环节（低通滤波器）可使得系统的性能得到改善。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所