[科普中国]-振型叠加法

以系统无阻尼的振型（模态）为空间基底，通过坐标变换，使原动力方程解耦，求解n个相互独立的方程获得各阶模态振型，进而通过叠加各阶模态振型的贡献求得系统的响应。

相关概念振型参与系数每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量（或者说该模态质量）之比，即为该振型的振型参与系数。一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大. 地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。 自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。 振型越高，周期越短，地震力越大，但由于我们地震反应是各振型的迭代，高振型的振型参与系数小。 特别是对规则的建筑物，由于高振型的参与系数小，一般忽略高振型的影响。

振型的有效质量这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的，不适用于一般结构。）。某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方。一个振型有三个方向的有效质量，而且所有振型平动方向的有效质量之和等于各个质点的的质量之和，转动方向的有效质量之和等于各个质点的转动惯量之和。1

基本特点（1）振型叠加法采用模态变换对原n自由度系统的运动方程解耦，将其解耦为非耦合的n个单自由度系统的运动方程；

（2）模态变换对系统的固有特性没有影响，而是以求解广义特征值问题为代价；

（3）对n个单自由度系统运动方程积分，比对联立方程组的直接积分节省时间，通常只要对这n个单自由度运动方程中的一小部分进行积分。但是采用振型叠加法需要增加求解广义特征值问题的计算时间，所以在实际计算中，究竟采用哪种方法，应根据具体情况确定；

（4）振型叠加法只适用于线性、时不变系统。若系统是非线性的，或者是时变的，则无法利用振型叠加法。

基本步骤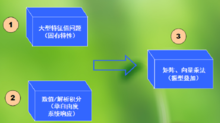

模态截断的必要性在用有限单元法进行结构动力分析时，结构的自由度数目有时十分巨大，会造成结构振动模态数目多且密集。根据实际计算经验:

(1)由于高阶模态中有较多的正负交变，因此有较多的结点位移为零;

(2)高阶模态的自振频率高，由于位移响应与自振频率的二次方成反比，因此位移响应小;

(3)从物理意义上看，结构体系中的高阶模态不易被激发，通常只有少数较低的模态会被激发，因此只需将自振频率低的几个模态进行叠加就可表达结构的振动状态。2

本词条内容贡献者为:

李晓林 - 教授 - 西南大学