[科普中国]-偏自相关函数

偏自相关函数是描述随机过程结构特征的一种方法。用Φkj表示k阶自回归式中第j个回归系数，则k阶自回归模型表示为xt=Φk1xt-1+Φk2xt-2+...+Φkkxt-k+ut。其中Φkk是最后一个系数。若把Φkk看作滞后期k的函数，则称Φkk，k = 1,2... 为偏自相关函数。它由下式中的Φ11 ,Φ22 ,...,Φkk组成：Xt=Φ11xt-1+ut；Xt=Φ21xt-1+Φ22xt-2+ut；......；Xt=Φk1xt-1+Φk2xt-2+......+Φkkxt-k+ut。因自相关函数中每一个回归系数Φkk恰好表示xt与xt-k在排除了其中间变量xt-1，xt-2，......，xt-k-1影响后的自相关系数，即xt-Φk1xt-1-Φk2xt-2-...-Φkk-1xt-k-1=Φkkxt-k+ut中的Φkk，所以偏自相关函数由此得名1。

偏自相关函数的定义用Φk1xt-1+Φk2xt-2+...+Φkkxt-k+ut，表示k阶自回归式中第j个回归系数，则k阶自回归模型表示为

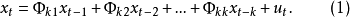
其中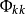是最后一个系数。若把看作滞后期k的函数，则称

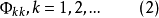为偏自相关函数。它由下式中的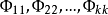组成。

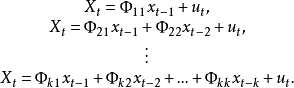
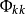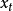因自相关函数中每一个回归系数恰好表示与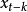在排除了其中间变量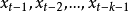影响后的自相关系数，即

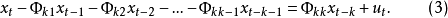中的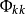，所以偏自相关函数由此得名1。

偏自相关函数求解用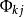表达Yule-Walker方程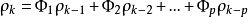，得，得

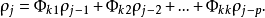用矩降形式表示上式：

或为：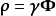

则:.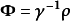

将k=1,2,...代人上式连续求解、可求得偏自相关函数

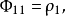
其中。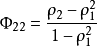

自回归模型的偏自相关函数对于AR(1)过程，当k=1时，≠0；当k>1时，=0，所以AR(1)过程的偏自相关函数特征是在k=1时出现峰值(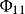=ρ1)，然后截尾，如图1所示。

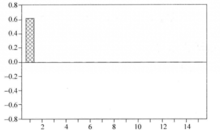
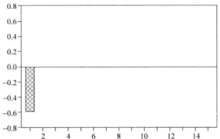
对于AR(2)过程，当k2时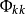，=0。偏自相关函数在滞后期2以后有截尾特性。

对于AR(p)过程，当k≤p时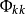，≠0；当k>p时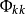；=0。偏自相关函数在滞后期p以后有截尾特征，因此可用此特征识别AR(p)过程的阶数1。

移动平均模型的偏自相关函数MA(1)过程的偏自相关函数呈指数衰减特征。若θ1>0，偏自相关函数呈交替改变符号式指数衰减；若θ1