[科普中国]-概率流

在量子力学里，概率流，又称为概率通量，是描述概率密度流动的物理量。假若将概率密度想像为非均匀流体。那么，概率流就是这流体的流率（概率密度乘以速度）。1

定义在量子力学里，从概率守恒可以得到“概率连续性方程”。设定一个量子系统的波函数为 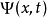。定义概率流 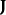为

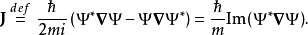其中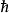， 是约化普朗克常数，m是质量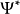，是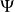是共轭复数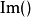，是取括弧内项目的复值。1

概率保守定律概率流满足量子力学的连续方程：

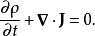其中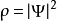，是概率密度。

应用高斯公式，等价地以积分方程表示，

；(1)

其中，V是任意三维区域，S 是V的边界曲面。这就是量子力学概率守恒定律的方程。

方程 (1) 左边第一个体积积分项目（不包括对于时间的偏微分），即是测量粒子位置时，粒子在V内的概率。第二个曲面积分是概率流出V的通量。总之，方程 (1) 表明，粒子在三维区域V内的概率对于时间的微分，加上概率流出三维区域V的通量，两者的总和等于零。

连续方程导引测量粒子在三维区域V内的概率P是

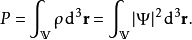
概率对于时间的导数是

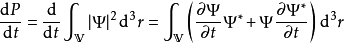；(2)

假设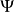的含时薛定谔方程为

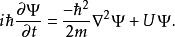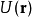其中，是位势。

将含时薛定谔方程代入方程 (2) ，可以得到

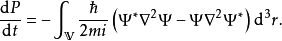应用一则矢量恒等式，可以得到

这方程右手边第一个项目与第三个项目互相抵销，将抵销后的方程代入，

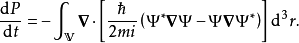将概率密度方程与概率流定义式代入，

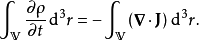这相等式对于任意三维区域V都成立，所以，被积项目在任何位置都必须等于零：

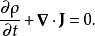
范例平面波设定一个粒子的波函数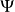为三维空间的平面波，2

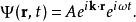其中，A 是振幅常数，k是波数，r是位置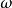，是角频率，t是时间。

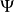的概率流是

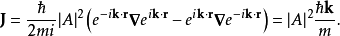这只是振幅的平方乘以粒子的速度。

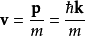请注意，虽然这平面波是定态，在每一个的地点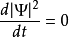，，但是概率流仍旧不等于0。因此可以推论，虽然概率密度不显性地跟时间有关，粒子仍可能移动于空间中。

盒中粒子思考一维盒中粒子问题，能级为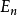的本征波函数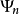是

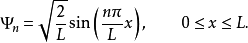其中，L是一维盒子的宽度，两扇盒壁的位置分别在x=0与 x=L 。

由于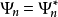，其概率流为

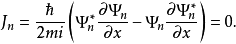
相关条目阶梯位势

透射系数

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所