[科普中国]-贝尔曼-福特算法

贝尔曼-福特算法（Bellman-Ford）是由理查德·贝尔曼（Richard Bellman） 和 莱斯特·福特 创立的，求解单源最短路径问题的一种算法。有时候这种算法也被称为 Moore-Bellman-Ford 算法，因为 Edward F. Moore 也为这个算法的发展做出了贡献。它的原理是对图进行V-1次松弛操作，得到所有可能的最短路径。其优于迪科斯彻算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高，高达O(VE)。但算法可以进行若干种优化，提高了效率。

简介贝尔曼-福特算法（英语：Bellman–Ford algorithm），求解单源最短路径问题的一种算法，由理查德·贝尔曼（Richard Bellman） 和莱斯特·福特创立的。有时候这种算法也被称为 Moore-Bellman-Ford 算法，因为Edward F. Moore也为这个算法的发展做出了贡献。它的原理是对图进行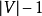 次松弛操作，得到所有可能的最短路径。其优于迪科斯彻算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高，高达 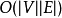。但算法可以进行若干种优化，提高了效率。

算法贝尔曼-福特算法与迪科斯彻算法类似，都以松弛操作为基础，即估计的最短路径值渐渐地被更加准确的值替代，直至得到最优解。在两个算法中，计算时每个边之间的估计距离值都比真实值大，并且被新找到路径的最小长度替代。 然而，迪科斯彻算法以贪心法选取未被处理的具有最小权值的节点，然后对其的出边进行松弛操作；而贝尔曼-福特算法简单地对所有边进行松弛操作，共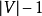 次，其中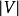 是图的点的数量。在重复地计算中，已计算得到正确的距离的边的数量不断增加，直到所有边都计算得到了正确的路径。这样的策略使得贝尔曼-福特算法比迪科斯彻算法适用于更多种类的输入。

贝尔曼-福特算法的最多运行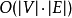 （大O符号）次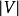， 和 分别是节点和边的数量）。

伪代码表示procedure BellmanFord(list vertices, list edges, vertex source) // 该实现读入边和节点的列表，并向两个数组（distance和predecessor）中写入最短路径信息 // 步骤1：初始化图 for each vertex v in vertices: if v is source then distance[v] := 0 else distance[v] := infinity predecessor[v] := null // 步骤2：重复对每一条边进行松弛操作 for i from 1 to size(vertices)-1: for each edge (u, v) with weight w in edges: if distance[u] + w