[科普中国]-普朗克单位制-

普朗克单位制是一种计量单位制度，由德国物理学家马克斯·普朗克最先提出，因此命名为普朗克单位制。这种单位制是自然单位制的一个实例，经过特别设计，使得某些基础物理常数的值能够简化为1。1

绪论普朗克单位制是一种计量单位制度，由德国物理学家马克斯·普朗克最先提出，因此命名为普朗克单位制。这种单位制是自然单位制的一个实例，经过特别设计，使得某些基础物理常数的值能够简化为1，这些基础物理常数是

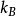
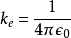
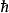万有引力常数G；约化普朗克常数；在真空里的光的光速c；库仑常数，其中是真空电容率，也就是电常数；玻尔兹曼常数。

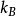
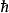上述每一个常数都至少出现于一个基本物理理论：G在广义相对论与牛顿的万有引力定律、在量子力学、c在狭义相对论、在静电学、在统计力学与热力学。实际上，以上的五个常数在许多物理定律的代数表达式中多次出现，因此引入普朗克单位制可以将这些代数表达式简化，普朗克单位制也因此成为了理论物理学一个非常有用的工具。在统一理论方面的研究，特别如量子引力学中，普朗克单位制能够给研究者一点大概的提示。

基本单位每一个单位制都有一组基本单位。（在国际单位制里，长度的基本单位是米）在普朗克单位制里，长度的基本单位是普朗克长度，时间的基本单位是普朗克时间，等等。这些单位都是由表1的五个基础物理常数衍生的。表2展示出这些基本普朗克单位。2

|| || 表1：基础物理常数

字键：L=长度，T=时间，M=质量，Q=电荷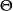， =温度。因为定义的关系，光速与库仑常数的数值是精确值，不存在误差。

|| || 表2：基本普朗克单位

使用普朗克单位后，表1的五个基础物理常数的数值都约化为1，因此表2的普朗克长度，普朗克质量，普朗克时间，普朗克电荷，与普朗克温度这些计量也都约化为1。这可以无量纲地表达为

因为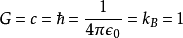，所以。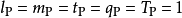

衍生单位在任何单位系统里，许多物理量的单位是由基本单位衍生的。表3展示了一些在理论物理研究里常见的衍生普朗克单位。实际上，大多数普朗克单位不是太大，就是太小，并不适合于实验或任何实际用途。

|| || 表3：衍生普朗克单位

简化物理方程严格地说，不同量纲的物理量，虽然它们的数值可能相等，仍旧不能用在相等式的两边。但是，在理论物理学里，为了简化运算，我们可以把这顾虑放在一边。简化的过程称为无量纲化。表4展示出普朗克单位怎样通过无量纲化使许多物理方程变得更简单。

|| || 表4：物理方程与其无量纲形式