[科普中国]-互谱密度函数

互谱密度函数(cross-spectral density function)是互相关函数的傅立叶变换。互谱密度函数一般与互相关函数具有同样的应用，但它提供的结果是频率的函数而不是时间的函数。这—事实大大开拓了使用范围，因此在可以应用相关分析的工程问题中大大增加了互谱方法的应用。互谱密度函数是有重要用途的，频谱分析中能用互谱的测量结果来识别动力系统的特性以及计算频响函数的振幅比和相位角1。

互谱密度函数的定义互谱密度函数的定义，数学上可描述为

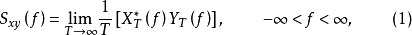
由于互谱密度函数的推导方法与自谱密度函数相同，它们的差别只是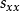是信号x(t)的自乘，而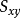是信号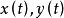与的互乘。应当注意的是，因为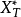与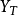一般不是互为共轭，所以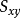为复数性质2。

互谱的单边谱为

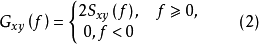由式(2)互谱密度函数也可以描述为

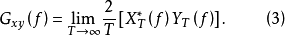
互谱密度函数的性质1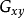．的数学属性

因为一般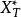与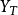是复数且不是互为共轭，所以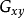为复数性质。

2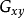．的共轭变量交换性

证明：

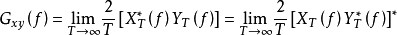
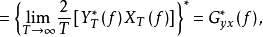式中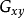：下标表示两个测量信号的随机变量x、y，该式表明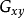，数值上等于两个信号x、y的信道互相交换后其应对的互谱密度函数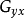取共轭的结果2。

3．互谱密度函数与互相关函数的关系

与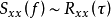关系类似，可以得到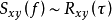也是一个傅里叶变换对，即有

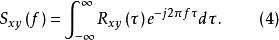
4．互谱密度函数的振幅和相位

1)共谱密度函数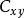和重谱密度函数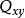

由互谱密度函数与互相关函数的关系得

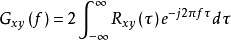
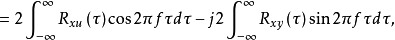
其中：共谱密度函数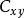为实部，重谱密度函数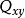为虚部。有

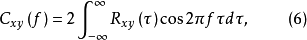
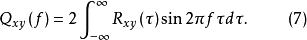
2)互谱密度函数的振幅和相位

由式(5)、式(6)和式(7)，可把互谱密度函数写成复数表示式，有

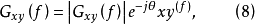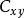式中：和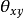分别为互谱密度函数的振幅和相位，有

振幅：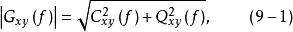

相位：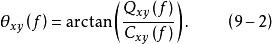

3)相位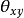的含义

由时域中的时延将引起频域中的相移，可推断出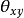的含义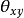：为反映信号y(t)相对信号x(t)时延方面的信息，为正，意味着在频率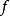处信号y(t)落后于信号x(t)，反之亦然2。

5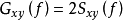．的证明

由傅里叶谱关于f=o轴共轭对称的性质，有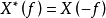和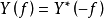，将它们的左边和右边分别相乘后，得

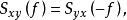再将互谱密度函数的共轭变量交换性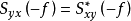代入上式，得

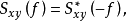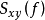由此看出，与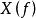一样，也具有关于f=0轴共轭对称的性质。根据互谱密度函数的振幅为取摸概念，对于双边谱的振幅有

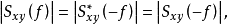取摸后为关于f=0轴对称，所以互谱的单边谱可描述为

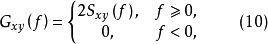互谱的单边谱为复数性质，也可描述为。

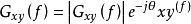本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所