[科普中国]-量子涨落

在量子力学中，量子涨落（英语：quantum fluctuation。或量子真空涨落，真空涨落）是在空间任意位置对于能量的暂时变化1。从维尔纳·海森堡的不确定性原理可以推导出这结论。

解释首先什么是涨落，比如我们测一根火柴棍的长度，测量了十次，每次都可能不一样，记作，我们可以对它们求个平均：

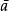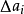每一次对火柴棍的测量和平均值有个偏差，即

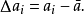
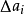可正可负，10个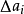描述了每次测量对测量平均值的偏离。有时我们希望用一个指标来描述对测量平均值的偏离，最直接的想法是用平均，即

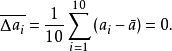
但由于每次偏离是随机的，如此定义的偏离的平均是0。合理的定义是对偏离的大小做平均，所谓偏离的大小是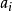偏离的绝对值。这可以看做是先平方再开方：

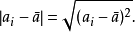
为什么不直接使用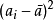，是因为这样做量纲就不对了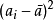，的量纲是面积，开方后才是长度。考虑到我们测量了十次，偏离的大小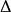定义为：

在以上例子中，每次测量的偏离就是涨落，而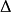就是对涨落大小的一个估计。

—————————————————————类比的分隔线——————————————————

正式开始解释什么是量子涨落。首先量子力学研究的是波函数：2

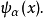
假如我们测量粒子的位置，粒子的位置在哪里我们也不知道，我们只知道粒子出现在位置x的几率密度是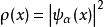。平均位置就是：

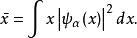
在量子力学中，粒子出现在任意位置都是有可能的，此时对平均位置的偏离是：

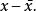
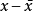可正可负，对上式求量子力学平均为0，

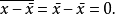
有意义的是偏离的大小，即绝对值：

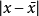
可以先对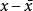求平方，再求量子力学平均，然后再开方注2：

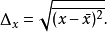
位置对量子力学平均值的偏离也叫涨落，涨落的大小由表征，由于这种偏离是由量子力学的本质特征——波函数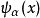决定，所以我们管这种涨落叫量子涨落。

意义量子涨落看似违反了能量守恒定律，但这种涨落发生在空间中的任何地方，而且能量存在的时间非常短，时刻一到，它就要消失，所以在大尺度上，能量守恒定律并没有被破坏。不过，上世纪60年代末，有人想到一种可能性：物质或能量的万有引力本身具有负的能量（因为引力是吸力，假设无限远的势能是0，那么当物体靠近后因为引力做功使得其势能为负值）。当涨落产生的能量产生的瞬间，它又产生了一个引力场，引力的负能量与物质（或能量本身）对应的正能量互相抵消，使整个系统看起来并没有多出能量，所以量子涨落没有违反能量守恒定律。1

相关算法量子退火（英语：Quantum annealing）是一种量子涨落特性的次经验算法，可以在目标方程拥有多组候选解答的情况下，找到全局最优解。量子退火主要用于解决离散空间有多个局部最小值的问题(组合优化问题)，像是寻找自旋玻璃的基态。

量子退火首先从具有相等权重的所有可能状态（候选状态）的叠加态开始，接着，系统随着含时薛定谔方程演化。根据横向场的时间依赖强度，导致了状态之间的量子隧穿，造成所有候选状态的机率幅不断改变，实现量子并行性。如果横场的变化速度足够慢，则系统保持接近瞬时哈密顿量的基态，即绝热量子计算。如果横场的变化速度加快，则系统可能暂时离开基态，但是在最终问题哈密顿量的基态下产生更高的可能性，即diabatic量子计算。横向场最终被关闭，且系统预计将达到与原来最优化问题的解相对应的经典易辛模型的基态。在最初的理论被提出之后，随即有了随机磁体量子退火成功的实验证明。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所