[科普中国]-伪随机数周期

伪随机数周期是指具有周期性循环往复的伪随机数列中不重复伪随机数的个数，或产生伪随机数迭代过程中一个循环所含数字个数。用某递推公式按一定程序产生伪随机数，一般从某—初始值起步产生伪随机数列x1，x2，…；若存在m，使对任意n，有xn+m=xn(n=1，2…)，则满足上述关系的最小m称做伪随机数的周期。选择产生伪随机数的递推公式时，要求周期充分长1。

基本介绍发生周期性循环现象的伪随机数个数，称为伪随机数的周期。

伪随机数亦称拟随机数、准随机数。按照不同于随机性原则的一定规则或程序，用数学方法通过选定的递推关系和迭代过程产生的，具们与随机数相似性质的数字。产生伪随机数的常用数学方法，有同余法、移位法、取中法、无理数的十进分解法....等。在数字计算机上用数学方法产生伪随机数，每到产生一定数量的伪随机数之后，出现循环重复的周期现象或退化为0的退化现象。对这类数学方法的一般要求为，1.产生伪随机数的周期一不重复伪随机数的数量一一应充分地长；2.产生随机数的速度要快，而所占用的内存要少；3.所产生的伪随机数具有所需要的统计性质——随机性和与给定分布律的一致性。严格地说，用任何数学方法迭代产生的伪随机数，都不是真正的随机数。不过在许多实际应用中，假如伪随机数的周期充分长，且通过相应的统计检验在一定显著性水平下可以认为，所得伪随机数满足随机性假设和与给定分布的--致性(拟合)假设，则这样的伪随机数可以代替随机数使用2。

伪随机数的周期和最大容量用来产生随机数的方法的数学方法，亦即用递推公式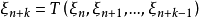：，对于给定的初始值，确定，经常遇到的是k=1情况，这时的递推公式是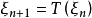，对于给定的初始值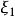，确定。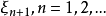

用数学方法产生的随机数存在两个问题

(i)递推公式和初始值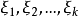 确定后，整个随机数序列便被唯一确定下来了。或者说，随机数序列中除前k个随机数是选定的外，任意一个随机数 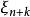，被前面的随机数唯一确定了,不满足随机数相互独立的要求。

(ii)的既然随机数序列是用递推公式确定的，而在电子计算机上所能表示的[0，1]上的数又是有限多的，因此，这样的随机数序列就不可能不出现重复地无限继续下去，一旦出现了这样的n'和n''，n'