[科普中国]-内曼分配

分层随机抽样中，各层中每个单位费用一样(即Ch=C)时样本单位的最优分配方法。内曼分配是一种不等概率样本设计，每个元素的抽样概率取决于其所在层的元素个数和样本量。

基本介绍内曼分配是分层随机抽样中，各层中每个单位费用一样(即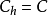)时样本单位的最优分配方法。设nh为各层的样本含量，Nh为h层单位总数，Sh为h层标准差，n为样本总含量(固定)，内曼(Neyman)1934年证明，当时，这种分配为最优分配即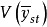达到最小值，因而命名为内曼分配。后来发现楚波罗(Tschuprow)1923年就给出了这一结论的证明1。

最优分配

最优分配是指在分层抽样中，在规定的抽样费用下配置各层的样本含量nh使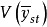达到最小值，或在给定的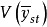条件下选择各层的样本含量nh使费用最少的一种样本单位分配方法。这样决定的各层的样本数为最优分配。可以证明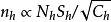。这里Nh为第h层的总体单位数，Sh为第h层的标准差，Ch为第h层的每单位调查费用。

相关说明此方法由著名统计学家内曼在1934年提出，故取名内曼分配。内曼分配是一种常用的非比例分层抽样方法，按此分配方法，第h层的样本量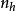为：

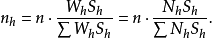
式中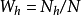，，N为总体元素总数，Nh为第h层的元素个数。

内曼分配是一种不等概率样本设计，每个元素的抽样概率取决于其所在层的元素个数和样本量。若层内采用简单随机抽样，则同层内的各元素的抽样概率相等，但不同层元素的抽样概率通常并不相等。第h层第i个元素的抽样概率为：

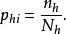
与比例分配公式进行比较可以看出，比例分配是内曼分配的一种特殊情况：若每个层的方差相等，内曼分配公式就演变为比例分配公式。显然，内曼分配不仅考虑了各层的元素数量，而且考虑了各层方差的大小：方差大的层多分配样本，方差小的层少分配样本。

与比例分配进行比较，内曼分配考虑了某个指标的方差因素，因此能够更有效地提高该指标以及与其相关程度较高的指标的抽样精度。

然而，比例分配的效果是比较稳定的，总是高于或至少等于同等样本量的简单随机抽样的精度，但内曼分配不具有这一特征，其效果可能高于比例分配，也可能低于比例分配，甚至低于简单随机抽样。例如，当一项调查有多个指标——多目标时就可能存在这种情况：一方面，对于某个或某些指标，内曼分配是很好的样本分配方法，抽样精度明显高于比例分配。另一方面，对于其他指标，内曼分配可能是一种很差的分配方法，抽样精度甚至可能低于同等样本量的简单随机抽样。此外，内曼分配的效果还会受辅助信息质量的影响，如果抽样框中的辅助信息与实际情况差异较大，预期的抽样精度与实际抽样精度会差异较大。

内曼分配的这些特点告诉我们，使用时要注意对其他指标抽样精度的分析、测算，避免顾此失彼，导致一些指标精度很高，另一些指标精度很低。同时要保证样本量有一定量的富余，以避免实际抽样精度明显低于预期抽样精度的情况发生2。

相关概念样本分配方法分层抽样的效果与分层的效果有关，同时与样本分配方法有关。如何在各层中分配样本，或者说不同分配方法，其产生的效果是不同的。分配方法有多种，在企业调查中最常用的是比例分配方法和内曼分配方法。

比例分配方法比例分配重在考虑层内的单位数，单位数多的层多分配样本，单位数少的层少分配样本。各层的单位数与样本单位数之比相等，也即在各层具有同样的抽样比。例如，总体共有N个企业，准备抽取n个企业；第h层的企业数为Nh，样本量为nh，按比例分配则要求：

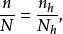或：

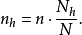
比例分配是一种等概率样本设计，即每个样本单位的抽样概率相等。若各层内采用简单随机抽样，则每个样本单位的抽样概率为：

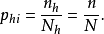
抽样理论告诉我们，采用比例分配的分层抽样，其抽样精度总是高于或至少等于同等样本量的简单随机抽样。或者说比例分配抽样的设计效应总是小于等于1，即deff≤1。

比例分配究竟能够在多大程度上提高抽样精度，则完全取决于层内各单位之间的差异程度。各层内单位的同质性程度越高——差异越小，比例分配抽样的效果越好。换句话说，层分得越好——各层内同质性程度越高，比例分配抽样在抽样精度上的获益越大。

分层抽样通过两种途径提高抽样精度：一是将单位差异较小或较为相近单位放在同一个层，减少层内方差；二是在总样本量不变的情况下，控制各层中的样本量。显然，采用比例分配时，抽样精度的获益主要来自于第一种途径，即同质性分层。然而在许多情况下，使用非比例抽样，给方差大的层多一些样本，而给方差小的层少一些样本，可以进一步提高抽样精度2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所