[科普中国]-内外表设计

内外表设计(orthogonal design by inside and outside array)亦称直积法，是一种试验设计。它是为考察一类因子对另一类因子的影响情况，用两张正交表垂直排列的一种试验设计。参数设计问题中恰有两类因子：可控因子类和噪声因子类，若把它们各放入一张正交表上，诸可控因子所在的正交表亦称为内表(inside array)；噪声因子所在的正交表亦称为外表(outside array)，然后把它们垂直排列形成直积表1。

基本介绍直积法设计是正交试验设计的一种改造。在某些工业试验设计中，所考察的因子常可分为两类：一类是配方因子，如原材料，配料比例等；另一类是工艺因子，如操作方法，加工条件等。直积法就是使每个配方因子的水平组合与每一工艺因子的水平组合相配合，从而研究它们之间交互作用的一种试验设计方法。

作为用户， 都希望得到质量特性非常稳定的物品。所谓质量特性稳定的物品， 就是在任何时间、任何环境中，使用起来都能持续正常地发挥功能的物品2。

这里所说的时间、环境，就是标示因素。把它列为实验条件，可以考察在它的影响下，控制因素是否稳定，也就是说，可以考察它与控制因素的交互作用。

在质量设计中，为考察标示因素的效应， 要用直积法进行数据分析。

所谓直积法，就是通过表的直积，把内侧正交表(简称内表)与外侧正交表(简称外表) 组合起来，进行实验或计算，以取得数据和分析数据的方法。

所谓内表，一般是指配列控制因素的正交表；所谓外表，一般是指配列信号因素、 误差因素、标示因素以及区组因素的正交表。但这在实践中，也不是绝对的，有时也可在内表中配列标示因素或其它因素2。

直积法的内、外表搭配关系，可示意如下:

|| || 表1 内外表设计

例题解析例 某化工产品提高收率的试验中，考察5个因素，A，B，C均为3水平因素，D，E均为2水平因素，因素水平表如2所示。显然A，B，C与D，E是两种性质不同的因素，前三者是配方因素，后两者是工艺因素。两类因素各自内部的交互作用可以忽略，但它们之间的交互作用A×D，A×E，B×D，B×E需加以研究3。

|| || 表2 因素水平表

解 这类问题通常要按照因素的性质分开做试验，先选择安排配方因素的正交表。称为内侧正交表或内表，将A，B，C3个3水平的配方因素安排在正交表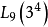 中，其表头设计如表3所示，按照该方案进行试验后会得到9个半成品。

|| || 表3 内表表头设计

再选择安排工艺因素的正交表，称为外侧正交表或外表，将D，E2个2水平的因素安排在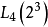 表中，其表头设计见表4。

|| || 表4 外表表头设计

进行试验时，让前面得到的9个半成品都按这个表头设计规定的工艺条件做4次试验，这样，一共做9×4=36个工艺条件试验。试验数据可用表5的形式列出。

|| || 表5 试验方案及数据

表中，y11代表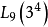的第1号条件下的半成品在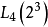的第1号条件下试验的数据，即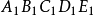下的试验结果，又如y43代表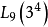的第4号条件下的半成品在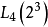的第3号条件下试验的数据，即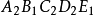下的试验结果，其余类推。

上述这种对试验的安排方法称为直积法，其特点是先把两种不同种类的因素单独安排试验，然后再把这两类因素组合试验，两类因素的组合简易，每个配方因素的水平组合与每一工艺因素的水平组合相配合。因而，可以分析因素间的交互作用，在操作上也比较简单易行3。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所