[科普中国]-状态估计

状态估计（state estimation）根据可获取的量测数据估算动态系统内部状态的方法。对系统的输入和输出进行测量而得到的数据只能反映系统的外部特性，而系统的动态规律需要用内部（通常无法直接测量）状态变量来描述。因此状态估计对于了解和控制一个系统具有重要意义。

简介状态估计是当代电力系统能量管理系统(EMS)的重要组成部分,尤其在电力市场环境中发挥更重要的作用。状态估计问题的提出激发了许多学者的研究兴趣,他们以数学、控制理论和其它新理论为指导,根据当时的计算机软件和硬件条件,结合电力系统的特点,在理论方面进行厂大量研究。同时,以状态估计软件实用为目标,针对实际工程面临的问题,探索和总结出许多可行的宝贵经验。状态估计的理论研究促进了工程应用,而状态估计软件的工程应用也推动了状态估计理论的研究和发展。迄今为止,这两方面都取得了大量成果。然而,状态估计领域仍有不少问题未得到妥善解决,随着电力系统规模的不断扩大,电力工业管理体制向市场化迈进,对状态估计有了新要求,各种新技术和新理论不断涌现,为解决状态估计的某些问题提供了可能1。

内容在确定性情形下，线性系统的状态估计的主要方法有吕恩伯格观测器。只有系统的能观测部分（见能观测性）的状态才能重构，而且能以任意快的速度来重构，但在具体实现时则受到噪声、灵敏度等因素的限制。在系统的装置或其观测通道受有随机噪声干扰时，则必须用统计估计方法来处理。依观测数据与被估状态在时间上的相对关系，状态估计又可区分为平滑、滤波和预报3种情形。为了估计t时刻的状态x（t），如果可用的信息包括t以前的观测值，就是平滑问题。如果可用的信息是时刻t的观测值，估计可实时地进行，称为滤波问题。如果必须用时刻（t－Δ）以前的观测来估计经历了Δ时间之后的状态x（t），则是预报问题。状态估计中所应用的方法属于统计学中的估计理论。最常用的是最小二乘估计，其他如风险准则的贝叶斯估计、最大似然估计、随机逼近等方法也都有应用。不管是维纳滤波还是卡尔曼滤波，这些方法都只适用于线性系统，而且需要对被估计过程有充分的知识。对于非线性系统或对动态系统特性不完全了解的复杂估计问题，还需要深入研究。工程上可用一些近似计算方法来处理，常见的有基于局部线性化思想的广义卡尔曼滤波器、贝叶斯或极大后验估值器和可以根据滤波过程的历史知识自动修改参数的自适应滤波或预报技术等。

状态估计器的估计准则状态估计的数学模型是基于反映网络结构、线路参数、状态变量和实时量测之间相互关系的量测方程:

z=h(x)+v

其中z是量测量;二是状态变量,一般是节点电压幅值和相位角;二是量测误差;二和二都是随机变量。

状态估计器的估计准则是指求解状态变量二的原则,电力系统状态估计器采用的估计准则大多是极大似然估计,即求解的状态变量二`使量测值z被观测到的可能性最大,用数学语言描述,即:

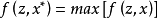
其中f(z)是量测z概率分布密度函数。

显然,具体的目标函数表达式与量测z的分布模式密切相关,对每个f(幼都有相应的极大似然估计函数。对同一系统的相同实时量测,若假定的量测分布模式不同,则得到的估计结果不完全相同,因此有不同估计准则的估计器1。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所