[科普中国]-区间分析

区间分析，又称区间数学，是一门用区间变量代替点变量进行运算的数学分支。它最初是从计算数学的误差理论研究发展起来的。1966年R.E.穆尔在《区间分析》一书中第一次系统提出区间运算理论。

区间分析的产生计算误差一直是数值分析中一个比较麻烦的问题，它来源于数据误差、截断误差和舍入误差。人们努力使计算结果保证在所要求的精度内；1然而，在许多问题中往往是推测计算结果的某种精度或者尽量使用高精度的运算以保证计算结果的精度，由于计算误差的累积可能使计算结果失去意义，区间数学提供了一种简便的方法，它考虑到各种误差，同时，作为计算结果，得到一个包含精确结果的区间，这就可能实现数值分析所希望解决的问题。

概念对于给定的数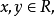：若满足条件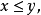则有界数集合

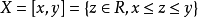就称为有界闭区间。其中，成为区间的下端点，成为区间的下断点，把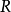上所有有界区间所构成的集合即为。

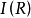性质1.区间运算满足结合律、交换律和常数运算；

2.两个相等区间相减不一定等于零区间；

3.区间分配律不一定成立。

应用20世纪70年代以来区间数学有很大发展，在计算数学方面有很多应用，如利用区间迭代法可判断对非线性方程组及算子方程解的存在惟一性及区间迭代序列收敛性，这是点迭代法得不到的结果。此外，它在区间插值与逼近、线性方程、非线性规划、微分方程等方面也有应用。2直接用区间量计算的计算机语言──区间语言也已出现。

应用一：

解常规方法很难解决的方程或方程组。

应用二：

处理工程中的模糊性、不完备性就要求代入区间值进行计算，涉及到区间方程的算法、区间方程组的解法以及区间扩张的控制。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所