[科普中国]-偏微分方程论

偏微分方程论(theory of partial differential e- quations)指包含多元函数的偏导数等式的偏微分方程，描述自变量、未知函数及其偏导数之间的关系。符合这个关系的函数是方程的解。偏微分方程分为线性偏微分方程与非线性偏微分方程，常常有几个解而且涉及额外的边界条件。

简介偏微分方程论是研究这类方程的一个数学分支学科，一般亦称为偏微分方程。客观世界的物理量一般可能表示成时间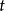 与空间位置坐标 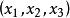的函数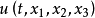 ，它的变化规律往往表现为它关于时间和空间坐标的各阶变化率之间的关系，即函数u与 的各阶偏导数之间的等式.

这样一类包含未知函数及其偏导数的等式称为偏微分方程。由几个偏微分方程所构成的等式组(未知函数也可以是几个)称为偏微分方程组。偏微分方程或偏微分方程组中所含偏导数的最高阶数称为此方程或方程组的阶。

发展在微积分理论形成不久的18世纪，人们就研究用微分方程来描述物理问题，并针对具体的物理问题求解。人们最早研究的是弦的横振动方程达朗贝尔(D'Alembert, J. 1e R.)最先得出它的通解;丹尼尔第一·伯努利 (Bernoulli , Daniel I)从弦的声音是由基音和泛音叠加而成的观点出发，认为方程的所有可能的解是的形状，其中l是弦长；达朗贝尔、欧拉(Eider, L. ) 和拉格朗日(I,agrange , J. -L.)还研究了两端固定的弦满足初始条件的解，并对解的允许函数进行了激烈的争论.欧拉和拉格朗日在流体力学的工作中，勒让德(Legendre, A. -M.)与拉普拉斯((Laplace , P. -S.)在天体力学的工作中都研究了调和方程。在流体力学的论文中，柯西(Cauchy,A.)得到了现在所称的柯西一黎曼方程组，欧拉得出了理想流体动力学方程组。

18世纪末，蒙日(Monge )开创了用几何解释偏微分方程的思想，对一阶和二阶非线性方程建立了完整的特征理论。19世纪，傅里叶(Fourier)系统研究了热传导方程，阐述了把有界区间上初边值问题的解表为三角级数或贝塞尔函数、勒让德函数的级数的一般分离变量法，对初值问题通过积分变换得出了解的表达式.他的工作不仅使微分方程的发展迈出了重要的一步，而且使人们把函数的概念从单个解析表达式中解放出来，促进了函数论、级数理论的发展，引起了人们对数学的逻辑基础的探讨。同时，还出现了许多现在以首创者命名的方程、公式和解法。例如，引力场的泊松方程、泊松公式、格林公式、格林函数，解二阶双曲型方程的黎曼方法，粘性流体运动的纳维一斯托克斯方程，柯西弹性力学方程组，电磁波的麦克斯韦方程组。这些成就对科学技术的发展起了巨大的推动作用，例如，麦克斯韦 (Maxwell , J. C.)预言电磁波以光速通过空间，断言光是电磁现象，鼓舞了洛伦兹(Lorentz,H. A.)关于电子的学说和爱因斯坦(Einstein, A.)关于相对论的研究。柯西给出了第一个关于解的存在定理，开创了偏微分方程的现代理论.杜·布瓦一雷蒙(Du Bois-Reymond , P. D. G.)提出把二阶线性偏微分方程分为椭圆、双曲和抛物三种类型.到19世纪末，二阶线性偏微分方程的一般理论已基本建立，偏微分方程或者称数学物理方程这一学科开始形成. 20世纪30年代起，各种泛函分析方法陆续被应用于偏微分方程的研究。20世纪40年代，绍德尔 (Schauder , J. P.)所采用的先验估计方法，不仅完满地建立了一般二阶线性椭圆型方程的古典解理论，而且为解决偏微分方程定解问题提供了非常有用的技巧。20世纪40年代末期出现的广义函数与索伯列夫空间理论，为偏微分方程理论的进一步发展提供了基本的工具。20世纪50到60年代，一方面作为线性分型方程理论的扩展和深人，一般线性偏微分算子理论得到了发展;另一方面，由于先验估计的深人发展，拟线性椭圆和抛物方程理论有了重大的进展，拟线性双曲方程(组)的间断解的研究也有许多好的成果。

近二三十年进展较快，且在当前国际上有较多人研究的偏微分方程问题有:在线性问题方面，微分算子的概念已先后推广为拟微分算子、傅里叶积分算子和仿微分算子，利用它们研究偏微分方程解的存在、解的光滑性、定解问题的惟一性、局部可解性、解的奇性传播与反射等问题，都取得了很好的结果。微局部分析方法是新发展起来的重要工具，利用它不仅解决了线性方程的许多新问题，且被逐步推广应用于处理非线性问题。在非线性问题方面，研究得较多的有拟线性与完全非线性椭圆及抛物方程、非线性双曲方程、孤立波、自由边界问题、反应扩散方程、多重解和分歧解等。研究中，不动点理论、拓扑度、变分方法(包括临界点理论)、上(下)解方法、单调算子理论、非线性半群、隐函数定理及变分不等式等方法和工具不断发展并得到了新的应用.微分流形上的偏微分方程的研究也取得了许多深人的结果，微分几何与偏微分方程的相互渗透成为一个重要的发展趋势。

偏微分方程偏微分方程中常以 为未知数及偏微分，如下：

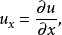
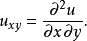用于空间偏微分的梯度运算子 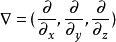，和时间偏微分 。

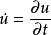常微分方程常微分方程是本科数学专业的核心基础课程，内容包括：微分方程建模、初等积分法、线性系统、常系数线性系统、若干振动问题、一般理论、定性理论初步。自微积分创立以来，人们就开始研究微分方程。从最初的初等求解技巧到今天日益发达的数值模拟技术，从早期对方向场的理解到今天关于微分方程定性理论、分岔理论的成熟知识体系，三百多年的历史使这门数学分支不仅成为了数学学科中队伍最大、综合性最强的领域之一，而且成为数学以外学科最为关注的领域之一。也正是因为科技发展对于微分方程的要求越来越强烈，所以各个学校都在结合自身的特点，开展一些教学上的改革，在课堂上展开多种形式的教学，力图使学生能够深刻理解微分方程所要传达的信息。

常微分方程课堂教学建设的主要内容，数学类各专业培养具有良好的数学基础和数学思维能力，受到数学建模、计算机和数学软件方面的基本训练，在数学和数学应用方面受到良好的教育，具有较高的科学素养和较强的创新意识，具备科学研究、解决实际问题及软件开发等方面的基本能力和较强的更新知识能力的综合人才。常微分方程课程是继数学分析、高等代数之后的一门重要基础课程，为学习泛函分析、偏微分方程等后继课程提供强有力支撑，也是应用性很强的一门课程，在实现数学、力学等专业培养目标中具有不可替代的重要作用。综合考虑该课程的特点，以及与其他相关课程的衔接问题，明确课程定位，确立本课程的具体目标为：（1）强化理论基础，服务后续课程；（2）强化建模思想和方法，鼓励学生思考，提高动手能力，培养创新意识。为此，加强课堂建设，需要从以下几方面入手1：

1.把课堂知识模块化，突出重点加强难点

2.采取灵活的教学模式，提高课堂教学质量

3.教学形式与手段的多样化，促进课堂教学

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所