[科普中国]-捕获再捕获抽样

捕获再捕获抽样是用于生态学以及估计野生动物总体数量的一种抽样方法。其基本方法是从总体中抽取一个样本，做上记号以后放回总体，使之与原总体的单位均匀地混合，经过适当的时间，再从中抽取一个样本。根据已做记号与未做记号的比率来推断总体的数量1。

基本介绍捕获-再捕获这一类抽样方法最初起源于对野生动物的调查，方法的步骤是：先抽取一定的样本，把这些单元做上记号，然后放回总体，使其与原总体的单元进行混合；再抽取一个样本，以观察其中做记号单元所占的比例，对总体单元数进行估计。

捕获再捕获抽样应用场合：总体单元数N是未知的，是需要估计的目标。如估计一个池塘中鱼的数量，一个森林中鸟类的数量，群众集会的参加人数等。

关于捕获再捕获抽样有很多模型，下面讨论其中的直接抽样法与逆抽样方法2。

相关知识捕获-再捕获(capture-recapture)技术是现在广为应用的技术，这是一种跨越概率抽样与非概率抽样的抽样技术，“跨越”一词是说这种技术超出概率抽样与非概率抽样的理论而又兼具两种抽样技术的特点。一方面，概率抽样一般基于有限总体规模，而且总体规模N已知，一旦总体的大小N本身无法知晓，诸如样本容量、抽样比之类的指标就无法得到，从而抽样设计以及估计量的计算都将无法进行，而捕获-再捕获技术恰恰超越了这一点，“竟然”可以用来估计总体规模的大小。另一方面，在进行捕获-再捕获的抽样设计过程中的许多步骤，比如两次抽样的容量大小以及估计总体大小的前提的假定，虽然都有研究人员的经验判断成分渗透在内，却一般都能给出估计的误差大小，这一点显然超出了非概率抽样的范畴。

捕获-再捕获技术的产生已有很长的一段时间，最初用于鱼类和野生动物总量的估计，又推广到流行病学问题的研究中，现今已经成为一种在很多领域都有广泛应用的调查与分析手段。在生态学中，捕获-再捕获方法多被称为彼得森方法或林肯方法，因为彼得森在1894年用做记号的鱼做过一些相关的研究工作，但这个方法真正被用于大规模的渔业研究则是由达尔在1917年实施的。1930年，林肯又巧妙地把这个方法用于估计鸭子总体的大小并获得了很大成功，随后萨卡和戴明继续将这种方法发扬光大，并在出生死亡率和估计现时人口总数等题目的研究上取得了引人注目的成就．萨卡和戴明的有关论文被公认为是将捕获-再捕获技术应用到人类健康领域的划时代成果。现今，应用捕获-再捕获技术的场合几乎无所不在，前提是只要能得到待研究总体的两个小规模子总体的单元名单2。

直接抽样法该方法首先从研究的数量N未知的总体中抽取一个随机样本，设样本量为t，将这些样本单元做上记号后放回总体，经过适当的时间以后，这些样本就与原总体均匀地混合在一起，很显然，这时做记号的数量占总体数量的比例为t/N=P，这里t是已知的，N是未知的，而P是待估计的，这就需要通过第二次抽样来估计，假设第二次抽样的样本量为n，而其中有记号的单元数为s，我们可以通过图1表示这一关系。

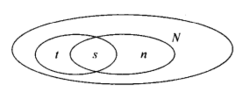
P的估计量为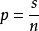 ，将这一估计量代人前面的公式，可以得到N的估计量为

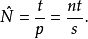显然，n要足够大，才能使得 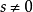，而且这里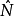 并不是N的无偏估计量。 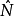的数学期望为

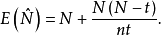但当第一次样本量t和第二次样本量n都足够大时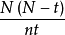， 就会逐渐变小，因此通常 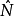是略有高估的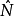， 的方差估计为

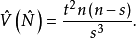在大样本的情况下，估计量 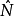也近似正态分布，可以利用正态分布做出一定置信度下的置信区间2。

逆抽样法在直接抽样法中提到，当s=0时，就无法对总体N作出估计，并且小比例抽样很容易出现这样的问题，为了避免这种情况的出现，一种方法是加大第一次抽样的数目，另一种方法就是霍尔丹提出的逆抽样的方法．这种方法在第二次抽样时，并不对n的数量作出规定，而是一直抽到曾做过记号的单元数达到s个为止，假设这时的样本量为n，那么P的估计量p仍为s/n，因此N的估计量仍为

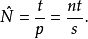
这与直接抽样法不同的是，逆抽样中s是预先规定的，而n是一个随机变量，这时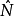 的方差估计为2

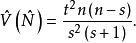
本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所