[科普中国]-能流密度矢量

坡印亭矢量（英语：Poynting vector），亦称能流密度矢量，其方向为电磁能传递方向，大小为能流密度（单位面积的能量传输速率）。坡印亭矢量的SI单位是瓦特每平方米（W/m^2）。它是以其发现者约翰·亨利·坡印亭来命名的。奥利弗·亥维赛和尼科莱·乌诺夫亦独立发现所谓的坡印亭矢量。

定义在坡印亭的原始论文和许多教科书中，它通常记作S或N，定义为

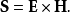其中E是电场强度；H是磁场强度。

这种形式通常被称为亚伯拉罕形式。偶尔也用电场强度E和磁感应强度B作为另一种定义。甚至可以把电位移矢量D和磁感应强度B结合起来得到的坡印亭矢量的闵可夫斯基形式，或使用D与H构成另一种形式。选用哪种形式一直是有争议的：罗伯特·费福（Robert Pfeifer）等人总结并一定程度上解决了亚伯拉罕与闵可夫斯基形式支持者之间长达一个世纪的争议。

坡印亭矢量表示的是电磁能量的能流矢量的特殊情况。然而，空间内任何形式的能量都有其移动方向，也有密度，所以其他形式的能量也可以定义能流矢量，例如机械能。1874年由尼科莱·乌诺夫发现的乌诺夫–坡印亭矢量以完全广义的观点描述了液体和弹性介质中的能流。1

微观领域的形式在某些情况下，可以更合适地定义坡印亭矢量为

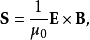其中μ0是真空磁导率；E是电场强度；B是磁感应强度。

可以直接从以总电荷和总电流为变量的麦克斯韦方程组和洛伦兹力定律导出这种形式。

对应的坡印亭定理的形式为

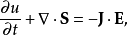其中J为全电流密度，而能量密度u为

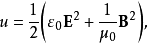其中 ε0是真空电容率。

坡印亭矢量的两种定义在真空或非磁性材料中等价，其中B= μ0H。在其他的情形，两者的差异在于S= 1/μ0E×B，而对应的u是纯辐射性的，因为耗散项−J⋅E包括了总电流，而以H场所做的定义涵盖了约束电流的贡献，因而缺乏耗散项。

推导S= 1/μ0E×B的过程中只需要微观场E和B，关于材料性质的假设则可回避掉。是故以此方式定义的坡印亭矢量与坡印亭定理是普遍成立的，不论是在真空中或各式各样的材料中。2

例子与应用同轴电缆举例而言，一条同轴电缆的介电绝缘体之中的坡印亭矢量与电缆的轴线几乎平行（假设电缆外无场，且包含直流电在内的波长远长于电缆直径）。输送到负载的电能完全是流经导体之间的介电质。极少量的能量是经导体流动，因为此处的电场强度接近于零。在导体内的能量流是径向的，成为导体电阻发热的能量散失。无能量流至电缆外，因为内层导体与外层导体所产生的磁场彼此相抵消。

电阻耗散若导体有不小的电阻，则在导体表面附近，坡印亭矢量则会出现歪斜而接触到导体。当坡印亭矢量伸入导体时，其被弯折到几乎与表面垂直的方向。此为斯涅尔定律以及导体内部甚慢的光速所造成的结果。

在导体内部，坡印亭矢量代表了能量从电磁场流入电缆，产生了电阻的焦耳发热。

静场在静态场考虑坡印亭矢量显示出了麦克斯韦方程组的相对论性，并让我们更加理解了洛伦兹力q(v×B)的磁分量。例如，考虑所附图片，它描述了在一个圆柱形电容器的坡印亭矢量，位于在由永磁体产生的一个磁场（指向纸内）。虽然只有静态电场和磁场，计算坡印亭矢量得出了顺时针方向循环流动的没有起始或结束的电磁能量。

虽然循环的能流看似是无意义或矛盾的，它却证明了保持动量守恒是绝对有必要的。动量密度与能流密度成正比，所以能量的循环流动包含着角动量。这是因为洛伦兹力的磁分量存在时，电容器放电。在放电过程中，能流中包含的角动量随着转移到穿过磁场的放电电流的电荷上而耗尽。1

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所