[科普中国]-猎物-捕食者模型

捕食者-猎物模型是一个简单而有价值的例子。该模型做了三个简单化假设：1）相互关系中仅有一种捕食者与一种猎物；2）如果捕食者数量下降到某一域值型以下，猎物数量就上升，而捕食者数量如果增多，猎物数量就下降。3）如果猎物数量上升到某一阈值，捕食者数量就增多，而猎物种数量就增多。如果很少，捕食者数量就下降。1

模型建立Lotka-Volterra(1925,1926)假设在没有捕食者时，猎物种群呈指数增长：

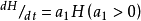
捕食者种群在没有猎物时呈指数下降：

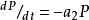
若两个种群置入有限空间时，猎物种群的增长率降低。降低的多少依赖于捕食者的密度：

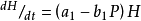
同样，捕食者种群的增长依赖于猎物种群的密度：

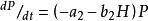
平衡点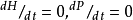 时

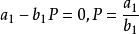
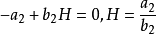
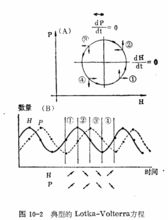
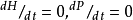系统的定性解为中心解，为周期性解。当种群初始值不时，以不同的封闭曲线围绕奇点(奇点即的点)星逆时针旋转(见图10-2)2

模型改进该方程显然有许多不足之处。例如：1）如无P，H呈指数增长。 2）H种群仅因P而死亡。3）P仅以H为食。4）两种群均无密度制约作用。故在原方程的基础上可做大量工作；改进一项或两项使之更符合生物学意义， 再进行定性分析。例如Volterra(1926) 设想无捕食者时(或寄生物，意义相同)，猎物种群服从逻辑斯蒂方程，其它不变。方程形式为:

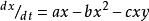
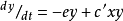
其中，第一式：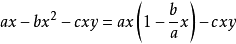

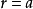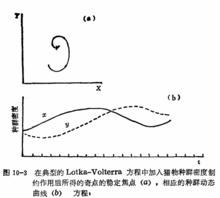
显然，逻辑斯蒂方程中的内禀自然增长率 ， 环境载力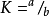 ，其奇点为稳定焦点。如图10-3(a)。Leslie和Gower (1948) 考虑到应加进去两个种群间的密度制约关系。方程如下：

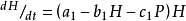
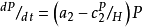
此方程中的第一式同于Volterra(1926)方程中的第一式，加入了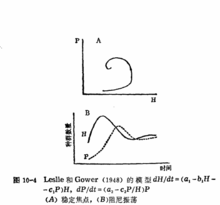猎物种群的自饱和项。

第二式中以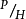 代替H，以体现当猎物少而捕食者多时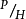， 值增大，不利于捕食者种群的增长。反之，若猎物多而捕食者少时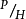， 值小，有利于捕食者种群的增长。

其奇点也为稳定焦点，如图10-4A。绘成种群曲线时(图10-4B)，两种群随时间而阻尼振荡，最后均达到平衡密度并共存下去。2

本词条内容贡献者为:

刘勇 - 副教授 - 西南大学资源环境学院