[科普中国]-多因素方差分析-

当有两个或者两个以上的因素对因变量产生影响时，可以用多因素方差分析的方法来进行分析。多因素方差分析亦称“多向方差分析”，原理与单因素方差分析基本一致，也是利用方差比较的方法，通过假设检验的过程来判断多个因素是否对因变量产生显著性影响。在多因素方差分析中，由于影响因变量的因素有多个，其中某些因素除了自身对因变量产生影响之外，它们之间也有可能会共同对因变量产生影响。在多因素方差分析中，把因素单独对因变量产生的影响称之为“主效应”；把因素之间共同对因变量产生的影响，或者因素某些水平同时出现时，除了主效应之外的附加影响，称之为“交互效应”。多因素方差分析不仅要考虑每个因素的主效应，往往还要考虑因素之间的交互效应。此外，多因素方差分析往往假定因素与因变量之间的关系是线性关系。从这个方面来说，方差分析的模型也是如下一个一般化线性模型的延续：因变量=因素1主效应+因素2主效应+…+因素n主效应+因素交互效应1+因素交互效应2+…+因素交互效应m+随机误差。所以多因素方差分析往往选用一般化线性模型(General Iinear Model)进行参数估计1。

多因素方差分析的概念多因素方差分析用来研究两个及两个以上控制变量是否对观测变量产生显著影响。多因素方差分析不仅能够分析多个控制变量对观测变量的独立影响，更能够分析多个控制变量的交互作用能否对观测变量产生显著影响，最终找到利于观测变量的最优组合2。

多因素方差分析的基本步骤多因素方差分析实质也采用了统计推断的方法，其基本步骤与假设检验完全一致2。

1．提出原假设

多因素方差分析的第一步是明确观测变量和若干个控制变量，并在此基础上提出原假设。

多因素方差分析的原假设是：各控制变量不同水平下观测变量各总体的均值无显著性差异，控制变量各效应和交互作用效应同时为0，即控制变量和它们的交互作用没有对观测变量产生显著影响。

2．观测变量方差的分解

在多因素方差分析中，观测变量取值的变动会受到三个方面的影响：第一，控制变量独立作用的影响，指单个控制变量独立作用对观测变量的影响；第二，控制变量交互作用的影响，指多个控制变量相互搭配后对观测变量产生的影响；第三，随机因素的影响，主要指抽样误差带来的影响。基于上述原则，多因素方差分析将观测变量的总变差分解为(以两个控制变量为例)：

SST=SSA+SSB+SSAB+SSE (1)

其中，SST为观测变量的总变差；SSA、SSB分别为控制变量A、B独立作用引起的变差；SSAB为控制变量A、B两两交互作用引起的变差；SSE为随机因素引起的变差。通常称SSA+SSB+SSAB为主效应，SSAB为N向(N-WAY)交互效应，SSE为剩余。其中，SST的定义为：

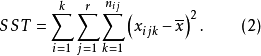式(2)中，k为第i控制变量的水平数；r为第j控制变量的水平数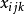；为控制变量A第i个水平和控制变量B第j个水平下第k样本值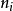；为控制变量A第i水平和控制变量B第j个水平下样本个数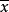；为观测变量均值。

SSA的定义为：

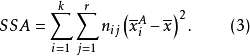式(3)中，nij为控制变量A第i个水平和控制变量B第j个水平下样本观测值个数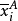，为控制变量A第i个水平下观测变量的均值。

SSB的定义为：

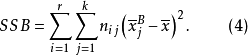式(4)中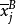，为控制变量B第j水平下观测变量的均值。

SSE的定义为：

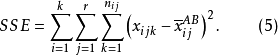
式(5)中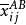，为控制变量A、B在i、j水平下观测变量的均值。于是，交互作用可解释的变差为：

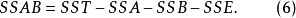3．比较观测变量总离差平方和各部分所占的比例，计算检验统计量的观测值和相伴概率P值

多因素方差分析的第三步是通过比较观测变量总离差平方和各部分所占的比例，推断控制变量以及控制变量的交互作用是否给观测变量带来了显著影响。容易理解，在观测变量总离差平方和中，如果SSA所占比例较大，则说明控制变量A是引起观测变量变动的主要因素之一，观测变量的变动可以部分地由控制变量A来解释；反之，如果SSA所占比例较小，则说明控制变量A不是引起观测变量变动的主要因素，观测变量的变动无法通过控制变量A来解释。对SSB和SSAB同理。

在多因素方差分析中，控制变量可以进一步划分为固定效应和随机效应两种类型。其中，固定效应通常指控制变量的各个水平是可以严格控制的，它们给观测变量带来的影响是固定的；随机效应是指控制变量的各个水平无法作严格的控制，它们给观测变量带来的影响是随机的。一般来说，区分固定效应和随机效应比较困难。由于这两种效应的存在，多因素方差分析模型也有固定效应模型和随机效应模型之分。这两种模型分解观测变量变差的方式是完全相同的，主要差别体现在检验统计量的构造方面。多因素方差分析采用的检验统计量仍为F统计量。如果有A、B两个控制变量，通常对应三个F检验统计量。

在固定效应模型中，各F检验统计量为：

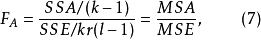
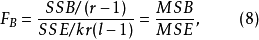
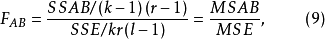
在随机效应模型中，FAB统计量同式(9)，其他两个F检验统计量为：

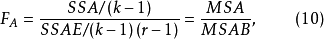
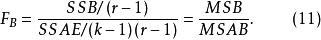SPSS自动计算F统计量，并依据F分布表给出相伴概率P值。

4．给定显著性水平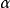，并做出决策

给出显著性水平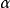，与检验统计量的相伴概率P值作比较。在固定效应模式中，如果FA的相伴概率P值小于或等于给定的显著性水平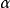，则应拒绝原假设，认为控制变量A不同水平下观测变量各总体均值有显著差异，控制变量A的各个效应不同时为0，控制变量A的不同水平对观测变量产生了显著影响；相反，如果FA的相伴概率P值大于给定的显著性水平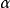，则不应拒绝原假设，认为控制变量A不同水平下观测变量各总体均值无显著差异，控制变量A的各个效应同时为0，控制变量A的不同水平对观测变量没有产生显著影响。对控制变量B和A、B交互作用的推断同理。在随机模型中，应首先对A、B的交互作用是否显著进行推断，然后再分别依次对A、B的效应进行检验2。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所