[科普中国]-严格决定对策

在有限二人零和对策中，称存在鞍点的对策为严格决定了的对策(称矩阵游戏更妥当)，简称严格决定对策(strictly determined game)，有些对策没有鞍点，有些则有许多鞍点。

基本介绍严格决定对策指在有限二人零和对策中，设局中人A和B的策略分别为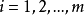 和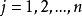 。如果设A选用策略i，B选用策略j时A的得分为 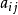( 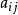为负时就是A的失分)，则能构造下面的得分表。

|| ||

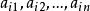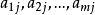如果A、B都互不知道对方所采取的策略，则A会选择使得的最小值即为最大的策略i，而B会选择使得的最大值即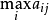为最小的策略j。假定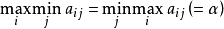， 如果A和B都采用最合理的策略，则A得到而B支付。具有上述条件的对策称为严格决定对****策，称为这个对策的值。当这一关系不成立时，就称为非严格决定对策1。

两人零和对策与严格决定对策人们在竞争或斗争中，总希望自己的一方取胜．每一方为取胜所作的努力一定会遭到对手的干扰，因此，任何一方都必须考虑对手可能怎样决策，从而选出自己的好的对策，这类竞争或斗争的现象，称为对策现象。

请看下面的矩阵游戏，设矩阵

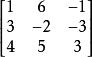为已知，甲可任选行数(可能是1，2，3)，乙也可选列数，当交错元素为正时，表示甲胜，当交错元素为负时，表示乙胜。例如，甲选第2行，乙选第3列，交错元素为-3，乙就获胜。甲、乙两人称为局中人，(甲选行数，乙选列数)组成一个“局势”，甲选某行是一个策略，甲可取3个策略；乙取某列也是一个策略，乙也可取3个策略，共可组成9个“局势”，胜负或得失是局势的函数。

有限零和两人对策是一种特殊的现象，局中人只有两个，每个可选取的策略只有有限个，且任一局势对应的得失之和总等于零，即一人所得即另一人所失。

有限零和两人对策可用矩阵表示，用下列矩阵

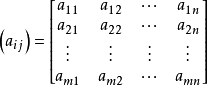表示甲的得失表，它表示甲共有m个策略(行数)，乙共有n个策略(列数)，写

在i行j列的数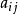 就是甲的得失，即当甲选取第i个策略、乙选取j个策略时，甲得 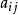(当它大于零时称得，当它小于零时实际上是失)。当然，乙的得失表即矩阵 。

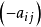例如，甲的得失表为

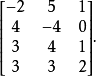如甲选第1行，他可能得到5分，但他也可能失去2分；如甲选第2行，他可能得到4分，但他也可能失去4分；如甲选第3行或第4行，都肯定能得分。同时，乙也会考虑他的对策。

甲的一种选择策略的办法是找出

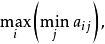即行中最小的数的集合中的最大者，它所在的行是较好的策略，上面这矩阵中，各行的最小值为 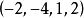，这里面的最大者是2。甲如选第4行，稳得2分。当行中最小数的集合中的元素都相等时，我们说 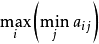不存在．

称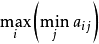 为鞍点，称存在鞍点的对策为严格决定了的对策(称矩阵游戏更妥当)。

有些游戏矩阵没有鞍点，有些则有许多鞍点，如

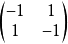无鞍点，又如

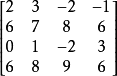有4个鞍点。

例如，齐王与田忌赛马的故事，齐王与田忌赛马，规定每人牵出强、中、弱马各1匹，共3匹组成马队进行团体赛，各队预先排好1，2，3次序，第1对第1，第2对第2，第3对第3，胜者得1分，可赢1干金，一场比赛下来，最多可得3分，最多失分也是3分。已知田忌的强马比齐王的强马差，但比齐王的中马好，田忌的中马比齐王的中马差，但比齐王的弱马好，田忌的弱马最差，齐王与田忌都有6种策略：

(1)(强中弱)；(2)(强弱中)；(3)(中强弱)；(4)(中弱强)；

(5)(弱强中)；(6)(弱中强)．

齐王的得失分表如下：

它不存在鞍点，不是严格决定了的对策。但确实存在一些局势，它们对应着齐王失1分，这故事中的确是田忌得了1分，齐王因此输了1干金2。

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学