[科普中国]-哈代-李特尔伍德定理

存在常数K>0及T0>0，使得对所有T>T0，黎曼ζ函数在临界线上0≤Im(s)≤T的区间内的非平凡零点数目不小于KT。这就是哈代-李特尔伍德定理，也称陈-哈代-李特尔伍德定理。早在1928年，陈建功就证明：三角级数绝对收敛的充要条件是它为杨氏(Young)连续函数的傅里叶级数。同年，G.H.哈代(Hardy，1877-1947)与J.E.李特尔伍德(littlewood，1885-1977)于德国数学时报上也发表了同一结论，因后者发行广泛，世人常称之为哈代-利特尔伍德定理。还其本源，此定理当称为“陈-哈代-李特尔伍德定理”。

相关介绍哈代一生除了对数学本身的卓越贡献外，还有两段与他人合作的经历在数学史上被传为佳话。其中一段是与印度数学奇才拉马努金(Srinivasa Ramanujan，1887-1920)的传奇性的合作，另一段便是与李特尔伍德的合作。李特尔伍德与哈代一样，是英国本土的数学家。英国的数学界自牛顿-莱布尼茨论战以来渐渐与欧洲大陆的数学界孤立了开来。1906年，当李特尔伍德还是剑桥大学三一学院(Trinity College)的一位年轻学生的时候，这种孤立所导致的一个有趣的后果落到了他的头上。他当时的导师、英国数学家巴恩斯(Ernest Barnes，1874-1953)在那年的暑期之前随手写给了他一个函数，轻描淡写地告诉他说这叫做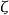 函数，让他研究一下这个函数的零点位置。初出茅庐的李特尔伍德不知 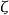函数为何方神圣，领命而去倒也罢了，但巴恩斯居然能漫不经心地把这样的课题交给当时还是“菜鸟”(尽管算是比较厉害的“菜鸟”)的李特尔伍德，说明他对欧洲大陆在近半个世纪的时间里对这一函数的研究，以及由此所显示的这一课题的艰深程度了解得很不够。

不过巴恩斯虽有对“敌情”失察之过，把任务交给李特尔伍德却是找对人了，因为李特尔伍德很快就成长为英国第一流的数学家。而在这过程中，巴恩斯所给的这个课题对他的成长不无促进之功。若干年后，当李特尔伍德终于体会到了黎曼猜想的艰深程度，甚至开始怀疑其正确性的时候，他并没有后悔当时曾经接下了这一课题，因为一位真正优秀的数学家在面对一个绝顶难题的时候，往往会被激发出最大的潜力及最敏锐的灵感。

事实上，拿到上述课题后的第二年，李特尔伍德就发现这个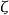 函数与素数分布之间存在着紧密关联。对于欧洲大陆的数学家来说，这种关联已不足为奇，因为它早在四十八年之前就被黎曼发现了。但在闭塞的英国数学界，欧洲大陆在这方面的工作当时还鲜为人知。不过闭塞归闭塞，例外还是有的，其中与李特尔伍德恰好同在三一学院的哈代就是一个例外。尽管李特尔伍德的发现在时间上未能领先，但他能独立地重复黎曼的部分工作，其功力之不凡还是给年长的哈代留下了深刻印象。此后李特尔伍德在曼彻斯特大学(University of Manchester)教了三年书。1910年他在获得了三一学院的教职后重返剑桥，由此开始了与哈代长达三十七年亲密无间的合作生涯，直到1947年哈代去世为止。

哈代与李特尔伍德的合作堪称数学史上合作关系的典范。在他们合作的极盛时期，欧洲数学界流传着许多有关他们的善意玩笑。

比如玻尔(玻尔一兰道定理中的玻尔)曾经开玩笑说当时英国共有三位第一流的数学家：一位是哈代，一位是李特尔伍德，还有一位是哈代-李特尔伍德。而与之截然相反的另一个玩笑则宣称李特尔伍德根本就不存在，是哈代为了自己的文章一旦出现错误时可以有替罪羊而杜撰出来的虚拟人物。据说兰道(玻尔一兰道定理中的兰道)还专程从德国跑到英国来证实李特尔伍德的存在性。

哈代与李特尔伍德对临界线上非平凡零点的研究起点与哈代定理相同。在哈代定理的证明中，着眼点是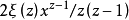 在整个临界线上的积分。这一着眼点其实已经为哈代定理的结果埋下了伏笔。正所谓“种瓜得瓜，种豆得豆”，既然所研究的是整个临界线上的积分，所得到的当然也就只是有关整个临界线上零点总数的笼统结果。

那么，为了得到能与黎曼猜想对非平凡零点的描述进行具体比较的结果，我们需要什么呢?我们需要的不仅是对整个临界线上零点总数的研究，更重要的是要了解临界线上位于区间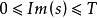 的零点数目。为此，哈代与李特尔伍德研究了 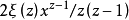在临界线上任一区间的积分，即

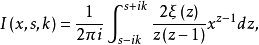其中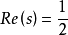 。通过对这一积分的细致研究，哈代与李特尔伍德发现临界线上不仅有无穷多个非平凡零点，而且虚部在0～T的零点总数随T趋于无穷的速度起码是KT(其中K为大于零的常数)。他们发表于1921年的这一结果在数学界并无确切名称，我们在这里将它称之为哈代-李特尔伍德定理，它的完整表述如下：

哈代一李特尔伍德定理：存在常数K>0及T0>0，使得对所有T>T0，黎曼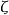 函数在临界线上 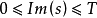的区间内的非平凡零点数目不小于KT。

有了这样的具体结果，我们就可以将它与黎曼猜想相比较了。那么，哈代-李特尔伍德定理距离黎曼猜想这一目标究竟有多远呢?为了回答这一问题，我们可以回忆一下黎曼那三个命题中的第一个，即：在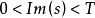 的区间内(不限于临界线上)，黎曼 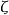函数的零点总数大约为 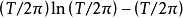。这个命题于1905年被曼戈尔特所证明，并且也是黎曼那三个命题中迄今唯一得到证明的命题。与这个命题相比，我们可以看到一个令人沮丧的结果，那就是哈代-李特尔伍德定理所给出的对临界线上非平凡零点数目下限的渐近估计相对于零点总数来说，其渐近比例为零!真是不比不知道，一比吓一跳，原来花了这么大工夫所得到的这一结果从纯比例的角度看竟是如此的“微不足道”。

这就是我们与黎曼猜想的距离所在，也是黎曼猜想的难度所在。

但尽管如此，哈代-李特尔伍德定理是有关黎曼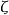 函数非平凡零点在临界线上的具体分布的第一个解析结果。在当时也是唯一一个那样的结果，其重要性是不言而喻的。哈代-李特尔伍德定理的这一纪录总共维持了21年，直到1942年才被赛尔伯格所打破1。

陈建功与哈代-利特尔伍德定理在三角级数的绝对收敛与绝对求和方面，陈建功也做出了卓越的贡献。早在1928年，他就证明：三角级数绝对收敛的充要条件是它为杨氏(Young)连续函数之傅里叶级数。同年，G.H.哈代(Hardy，1877-1947)与J.E.李特尔伍德(littlewood，1885-1977)于德国数学时报上也发表了同一结论，因后者发行广泛，世人常称之为哈代-利特尔伍德定理。还其本源，此定理当称为“陈-哈代-李特尔伍德定理”。陈建功在三角级数的收敛与求和方面还有许多贡献，难以一一列举，但必须指出，他1944年的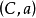求和的结果推进了哈代-利特尔伍德的定理2。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学