[科普中国]-抽象自动机

抽象自动机是—种能够识别语言的抽象装置，它不是具有物理实体的机器，而是表示计算机运算方式的抽象的逻辑关系系统，这样的抽象自动机可以用来检验输入的符号串是不是语言中合格的句子：如果是合格的句子，自动机就接收它，如果不是就不接收它。 数理语言学中，研究抽象自动机的理论称为自动机理论1。

基本介绍抽象自动机是一种能够识别语言的抽象的装置，它不是具有物理实体的机器，而是表示计算机运算方式的抽象的逻辑关系系统，这样的抽象自动机可以用来检验输入的符号串是不是语言中合格的句子，如果是合格的句子，自动机就接收它，如果不是，就不接收它，如图所示：

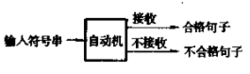
数理语言学中研究抽象自动机的理论称为自动机理论(automata theory)。

抽象自动机的分类自动机可分为有限自动机（即时序机）、后进先出自动机（即下推自动机）、线性有界自动机、图灵机等几种。它们对语言的识别能力各不相同。

自动机理论是以研究离散数学系统的结构、功能以及两者之间关系为主要内容的数学理论。自动机有11种: 有限自动机、下推自动机、线性有界自动机、图灵机、时序机、波斯特机、随机存取机、堆栈自动机、无线自动机、概率自动机和细胞自动机。

常见自动机有以下几种：以电话交换机为主要实例的有限自动机，是自动机理论的基础，被应用到自动控制、生物系统中；由下推表组成的单项非确定程序的下推自动机；线性有界自动机；用来描述通用计算机计算能力的图灵机模型；进行与转移函数，转移状态有关输出的时序机；由一些基本语句构成程序框图的波斯特机；随机存储机；堆栈自动机；不受有限自动机做控制器和存储限制的无限自动机；统计自动机某一条件概率分布的概率自动机和细胞自动机。

有限自动机有限自动机(finite automaton)亦称时序机，有限离散数字系统的抽象数学模型。一个有限自动机M由五元组(X，Y，S，δ，λ)给定，其中X，Y和S都是非空有限集，分别称为M的输入集、输出集和状态集；δ是笛卡儿积集合S×X到S的映射，称为M的下一状态函数；λ是S×X到Y的单值映射，称为M的输出函数，当δ是单值映射时，称M为确定型有限自动机；当δ是多值映射时，称M为非确定型有限自动机。有限自动机有三种功能：作为序列转换器，将输入序列变换为输出序列;作为序列识别器，识别输入的序列是否具有某种性质；作为序列产生器，产生具有所要求性质的序列2。

研究有限自动机的功能、结构以及两者关系的数学理论称为有限自动机理论。有限自动机理论的基本内容包括逻辑网络、状态化简、状态分配、神经网络和有限识别器等。

1.逻辑网络。基本的逻辑元件按是否具有记忆功能，可以分为记忆元件(如触发器和延迟器等)和组合元件(如各种与、或、非门等)两类。把一些基本逻辑元件按一定要求连结起来，就组成逻辑网络。若把逻辑网络中进入记忆元件的输入线去掉后所得网络不再含有回路，则称这样的网络为合式网络。不含记忆元件的合式网络称组合网络。逻辑网络比组合网络复杂。在工程实现上，要求对于一个给定的有限自动机建立和实现此有限自动机的逻辑网络。已经证明任何合式网络的功能都可以用一个有限自动机来描述;任何一个有限自动机描述的功能也都可以用合式网络来实现。

2.状态化简。对任何有限自动机都惟一(在同构意义下)存在一个状态数目最少的有限自动机与它等价。根据有限自动机理论，对给定的有限自动机，可有效地求出与之等价的最简形式的有限自动机。

3.状态分配。要构造具有多个状态的网络，需要使用多个基本记忆元件，利用这些记忆元件的各种状态组合来表示不同的状态。一般地，不同的状态分配导致逻辑网络具有不同的复杂程度.如何选择较好的分配方案，使逻辑网络的构造尽可能地简单，是有限自动机研究的一个主要课题。

4.神经网络。1943年，麦克卡洛克(Mcculloch)和皮特斯(W.Pitts)提出的神经网络模型是有限自动机的一个实例。1951年，克林(S.C.Kleene)在这种神经网络模型的基础上，提出了正则事件(正则语法)的概念，证明了正则事件是可以被神经网络或有限自动机表示的事件，而且神经网络或有限自动机可以表示的事件也一定是正则事件。

5.有限识别器。在形式语言理论中，有限自动机通常作为语言的识别器来使用。作为识别器，有限自动机的输出可以被忽略，而由最后达到的状态去决定输入序列是否具有给定的性质，这种有限自动机也称为有限接收机。按其下步状态是否完全确定，有限识别器可分为确定型和非确定型两种，它们分别与确定型和非确定型有限自动机相对应，它们也都接受同一类语言，即正则语言2。

概率自动机概率自动机(probabilistic automaton)亦称随机自动机，一种自动机。是所处环境或内部具有有限或无限的随机因素的自动机，与非概率型自动机的主要区别是：概率自动机的动作是随机的.每个概率自动机一般都需规定两组概率：一是给定自动机的初始状态的概率分布——初始分布，一般用一个随机矢量表示;二是规定在自动机处于某一状态，并向自动机输入某个字母的条件下，自动机下一动作(如状态转移、输出某个字母、改写字母等)的条件概率函数。有了这两组概率，就可计算自动机到达某个最终状态的概率，包含有不可靠元件的数字电路和通信的信道都可以表示为概率自动机。

细胞自动机细胞自动机(cellular automaton)是一种自动机，是有限细胞空间形式的自动机，常作为并行计算机的一种理论模型，细胞空间概念是冯·诺伊曼(J.von Neumann)在20世纪50年代初期研究自繁殖自动机的逻辑问题时提出的，细胞自动机由许多细胞(或单元)构成。每个“细胞”是一台计算机的模型，都有自己的存储器，都具有输入、加工和输出数据的能力。细胞和细胞之间有邻接关系，有些模型还和外部相连，以便与外部交换输入输出数据。冯·诺伊曼细胞自动机是最早最基本的自动机，其他各种类型的细胞自动机(如L系统)都是由冯·诺伊曼自动机推广而来的。细胞自动机除了在形式上可作为并行计算机的理论模型来研究外，还可以作为语言(被机器接受的输入字的集合)识别器，用于模式识别.此外，它对于大规模集成电路的设计方法也具有重要的意义。

下推自动机下推自动机(pushdown automaton)亦称后进先出自动机，一种自动机。是能控制一条输入带和一个栈的有限自动机。栈也称为“后进先出”表，即符号的写入或取出只能在表的顶端进行。在文法结构数学模型中，下推自动机可以用作上下文无关语言的识别接受器。下推自动机(简称PDA)可以形式地定义为一个7元组P=(Q，Σ，Γ，δ，q0，Z0，F)，其中：

1.Q是一个有限的状态集合；

2.Σ是一个有限的输入字母表；

3.Γ是一个有限的栈字母表；

4.δ是一个从Q×(Σ∪{e})×Γ到Q×Γ*的有限子集的映射；

5.q0在Q中，是有限控制的初始状态；

6.Z0在Γ中，是一个称为栈底的符号；

7.F⊆Q，是终结状态集合。

下推自动机是一个非确定的装置，对于有限自动机，确定型和非确定型有限自动机在接受语言上是等价的。这一结论对于下推自动机是不成立的。非确定型下推自动机接受的语言集合是上下文无关语言；确定型下推自动机接受的语言集合是非确定型下推自动机接受的语言集合的真子集，称为确定型上下文无关语言。

图灵机图灵机(Turing machine)是一种抽象计算模型，是20世纪30年代中期英国数学家图灵(A.M.Turing)首先提出来的，用来精确定义可计算函数，图灵机由一个控制器、一条可无限延伸的存储带和一个读写头组成，它所能进行的操作为：

1.左移(读写头在存储带上向左移一格)；

2.右移；

3.在存储带的某一格内写下或清除一个符号；

4.条件转移等。

图灵机的结构虽然比较简单，但在理论上它却能够模拟现代数字计算机的一切运算，因此可看作是现代数字计算机的一种数学模型。可以通过对这种模型的研究来揭示数字计算机的性质.可以证明，存在一个图灵机U，它可以模拟任何其他图灵机，这样的图灵机U称为通用图灵机。通用图灵机正是后来出现的存储指令的通用数字计算机的理论原型.图灵机所定义的语言类称为递归可枚举集.图灵机所计算的整数函数类称为部分递归函数。图灵机在计算能力上等价于递归函数、波斯特系统等其他计算模型。

线性有界自动机线性有界自动机(linear bounded automaton)是一种图灵机(参见“图灵机”)，是把计算限制在仅仅包含输入的那一段带上的图灵机，可用作上下文有关语言的识别接受器。线性有界自动机(缩写为LBA)可形式地由M=(K，Σ，Γ，δ，q0，F)来表示，其中：K是状态的有限集；Γ是带符号的有限集；Σ⊆Γ是输入符号集；K中的q0是起始状态；F⊆K是终结状态集；δ是从K×Γ到K×Γ×{L，R}子集的映射，(L，R)分别是读写头左右移一格。Σ含有两个特殊的符号，通常记为￠和$，它们分别是左端标志和右端标志。这些符号开始就处在输入带的端点，其作用是阻止带头离开带上出现符号的区。

确定型和非确定型图灵机接受的语言是相同的，但是，已知非确定型线性有界自动机(以NDLBA表示)接受的语言类正好是上下文有关语言。确定型线性有界自动机(以DLBA表示)的功能不会超过NDLBA的，以不等式表示为

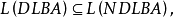其中L表示该类自动机接受的语言集合，至今人们仍未能把包含关系精确为真包含关系或相等关系，这是一个著名的尚未解决的问题，简称LBA问题2。

自动机理论自动机理论(automaton theory)是关于自动机的功能、结构及两者关系的数学理论。自动机是一个数学概念，它是离散数字系统的抽象模型，这里所说的离散数字系统，乃是一种动态系统，它的变量是数字量，时间是离散的。例如，数字电路和算法就是两个典型的离散数字系统。自动机理论的主要研究课题是分析和综合问题：给出一个具体的自动机的结构，分析它的功能；给出自动机的功能描述，综合出能实现此功能的自动机的结构。

自动机理论是理论计算机科学中较早形成的部分，早在1850年，英国布尔(G.Boole)就在用数学方法研究思维规律的问题时，建立了逻辑代数。1948年，美籍匈牙利数学家冯·诺伊曼(J.von Neumann)提出建立自动机的一般逻辑理论。20世纪50年代，在开关网络理论和数理逻辑中图灵机理论的基础上，形成了自动机理论这一数学分支学科。20世纪50年代以来，自动机理论有了深入的发展和广泛的应用。自动机理论大致可分为以下五个次级学科：

1.有限自动机理论：主要研究对象为开关网络、数字电路、计算机这类存储量有限的自动机；

2.无限自动机理论：主要研究对象为算法和理想计算机这类存储量不受限制的自动机；

3.概率自动机理论：主要研究对象是在环境或内部具有随机因素的自动机；

4.细胞自动机理论：主要研究对象是由许多互连的小自动机并行运算形成的大自动机；

5.抽象自动机理论：将自动机作为一种数学系统，研究自动机的一般数学性质。

自动机理论与数理逻辑、可计算性理论、计算复杂性理论、形式语言理论、控制论等数学分支都有关系，特别是它与形式语言理论关系密切。一方面自动机作为形式语言的一种主要描述方法，另一方面形式文法也可作为自动机识别集的一种描述方法。自动机理论在自动控制、计算机和数字通信等领域有着广泛的应用2。

美国语言学家N.乔姆斯基等人建立了形式文法和自动机之间的联系，证明语言的形式文法与自动机之间存在着如下的对应关系：①若某一语言能用图灵机来识别，则它就能用O型文法生成，反之亦然；②若某一语言能用线性有界自动机来识别，则它就能用上下文敏感文法生成，反之亦然；③若某一语言能用后进先出自动机来识别，则它就能用上下文自由文法生成，反之亦然；④若某一语言能用有限自动机来识别，则它就能用有限状态文法生成，反之亦然。

这种关于形式文法与自动机的关系。反映了语言的生成过程与识别过程的内在联系，它已成为计算机科学的基石之一，这是语言学对于现代自然科学发生影响的一个明证3。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学