[科普中国]-确定型有穷自动机

有穷自动机的每一步操作都是确定的，因此可称为确定型有穷自动机。确定有穷自动机就是说当一个状态面对一个输入符号的时候，它所转换到的是一个唯一确定的状态。

简介引入有穷自动机是一种有穷级数模型。它由一个读头和一条有穷长的纸带所组成，纸带被分割成有限个同样大小的单元，每个单元中可以是空的，或写有取自有穷字母表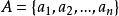 上的一个字母，读头在每一时刻都对准一个单元，并具有一个确定的内部状态，这些内部状态构成一个有穷集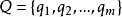。其中指定一个（比如 q1）为初始状态，另外，指定一个 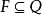作为终止状态（或接受状态）集。

读头每次只能向右移动一单元（而不能写或抹），并且每次都必须向右移动。读头所取的内部状态将由一个转换函数 δ 所确定。具体地说，在一个有穷自动机 𝒜 工作时，当读头所指单元内符号为 ai，内部状态为 qi 时，读头将向右移一单元并取新的内部状态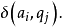于是，有穷自动机𝒜 可以形式地看成右字母表 A，内部状态集 Q、开始状态 q1、终止状态集 F 及转换函数 δ 所组成的一个五元组 𝒜= 。在纸带上给定 A 上的一个字 δ，如约定读头指向 σ 最左边的符号且以 q1 为开始状态，𝒜 便可开始运行，当 𝒜 读完 σ 的读头所取的内部状态为接受状态，则称 𝒜 接受 σ ，否则便拒绝 σ 。所有被 𝒜 所接受的字组成的 𝒜 接受的语言 L(𝒜)={σ∈A*|𝒜 接受σ}。

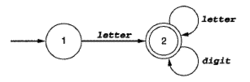美国逻辑学家、数学家克林(Kleene,S.C.)证明了一个语言可被某有穷自动机接受，当且仅当它为正规的，这个结论成为克林刻画。

定义有穷自动机的每一步操作都是确定的，因此可称为确定型有穷自动机。如果允许在每一步上读头的内部状态可在几个状态中任取，即 δ 之值为内部状态之集合（而不是一个内部状态），这样便得到非确定型有穷自动机。但是这两类自动机接受的语言类时一致的。1

辨析确定有穷自动机就是说当一个状态面对一个输入符号的时候，它所转换到的是一个唯一确定的状态；

不确定有穷自动机是说当一个状态面对一个输入符号的时候，它所转换到的可能不只一个状态，可以是一个状态集合。这就是两者的主要区别。还有就是 DFA 的开始状态是唯一的，而 NFA 的开始状态是一个开始状态集。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学