假设对于两个不同的可观察量 A 和B做测量,改变测量顺序,例如从AB改变为BA,则可能直接影响测量结果。假若测量结果有所不同,则称这两个可观察量为不相容可观察量;否则,称这两个可观察量为相容可观察量。以数学术语表达,两个不相容可观察量A和B的对易算符不等于零
简介量子力学与经典力学的一个主要区别,在于怎样理论论述测量过程。在经典力学里,一个物理系统的位置和动量,可以同时被无限精确地确定和预测。在理论上,测量过程对物理系统本身,并不会造成任何影响,并可以无限精确地进行。在量子力学中则不然,测量过程本身会对系统造成影响。
怎样才能正确地理论描述对于一个可观察量的测量?设定一个量子系统的量子态,首先,将量子态分解为该可观察量的一组本征态的线性组合。测量过程可以视为对于本征态的一个投影,测量结果是被投影的本征态的本征值。假设,按照某种程序制备出一个系综,在这系综里,每一个量子态都与这量子态相同,现在对于这系综里的每一个量子态都进行一次测量,则可以获得所有可能的测量值(本征值)的机率分布,每个测量值的概率等于量子态处于对应的本征态的概率幅的绝对值平方。
因此,假设对于两个不同的可观察量A和B做测量,改变测量顺序,例如从AB改变为BA,则可能直接影响测量结果。假若测量结果有所不同,则称这两个可观察量为不相容可观察量;否则,称这两个可观察量为相容可观察量。以数学术语表达,两个不相容可观察量A和B的对易算符不等于零:
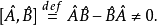 1
1
可观察量在物理学里,特别是在量子力学里,处于某种状态的物理系统,它所具有的一些性质,可以经过一序列的物理运作过程而得知。这些可以得知的性质,称为可观察量(observable)。例如,物理运作可能涉及到施加电磁场于物理系统,然后使用实验仪器测量某物理量的数值。在经典力学的系统里,任何可以用实验测量获得的可观察量,都可以用定义于物理系统状态的实函数来表示。在量子力学里,物理系统的状态称为量子态,其与可观察量的关系更加微妙,必须使用线性代数来解释。根据量子力学的数学表述,量子态可以用存在于希尔伯特空间的态矢量来代表,量子态的可观察量可以用厄米算符来代表。2
不相容可观察量假若两种可观察量的对易算符不等于0,则称这两种可观察量为“不相容可观察量”:
 其中,
其中,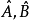 分别是可观察量A、B的算符。
分别是可观察量A、B的算符。
这两种算符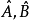 绝对不会有共同的基底。一般而言,
绝对不会有共同的基底。一般而言,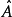 的本征态与
的本征态与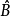 的本征态不同假设量子系统的量子态为
的本征态不同假设量子系统的量子态为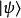 。对于算符
。对于算符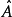 ,所有本征值为
,所有本征值为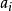 的本征态
的本征态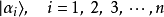 ,形成一个基底。量子态
,形成一个基底。量子态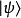 可以表示为这组基底本征态的线性组合:
可以表示为这组基底本征态的线性组合:
 其中,
其中,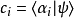 是复系数,是在量子态
是复系数,是在量子态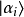 里找到量子态
里找到量子态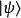 的概率幅。
的概率幅。
对于算符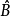 },所有本征值为
},所有本征值为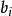 的本征态
的本征态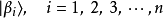 ,形成了另外一个基底。量子态
,形成了另外一个基底。量子态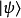 可以表示为这组基底本征态的线性组合:
可以表示为这组基底本征态的线性组合:
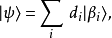 其中,
其中,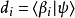 是复系数,是在量子态
是复系数,是在量子态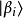 里找到量子态
里找到量子态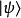 的概率幅。
的概率幅。
对于量子系统的可观察量A做测量,可能得到的结果是各种本征态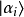 的本征值
的本征值 ,获得这些不同结果的机会具有概率性,可以表达为概率分布,结果为
,获得这些不同结果的机会具有概率性,可以表达为概率分布,结果为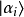 的概率是
的概率是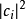 。
。
假设测量的结果是本征值 ,则可以推断,在测量之后短暂片刻内,量子态是本征态
,则可以推断,在测量之后短暂片刻内,量子态是本征态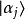 。假若立刻再测量可观察量A,由于量子态仍旧是本征态
。假若立刻再测量可观察量A,由于量子态仍旧是本征态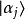 ,所得到的测量值是本征值
,所得到的测量值是本征值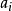 概率为1。假若立刻再对本征态
概率为1。假若立刻再对本征态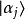 测量可观察量B,则会得到统计性的答案。假设测量的结果是本征值
测量可观察量B,则会得到统计性的答案。假设测量的结果是本征值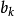 ,则可以推断,在测量之后短暂片刻内,量子态是本征态
,则可以推断,在测量之后短暂片刻内,量子态是本征态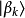 。
。
根据不确定性原理,
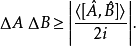 设定
设定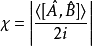 。假设,A与B是两个不相容可观察量,则
。假设,A与B是两个不相容可观察量,则 。而A的不确定性与B的不确定性的乘积
。而A的不确定性与B的不确定性的乘积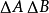 ,必定大于或等于
,必定大于或等于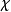 。1
。1
参阅位置算符
动量算符
角动量算符
哈密顿算符
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国