[科普中国]-半正定埃尔米特二次型

正定埃尔米特二次型是与实数域上正定二次型相对应的概念。正定、半正定、负定、半负定的埃尔米特二次型统称为定型的；不定的埃尔米特二次型称为不定型的。

简介正定埃尔米特二次型是与实数域上正定二次型相对应的概念。

对于变量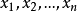 的任何复数值，埃尔米特二次型 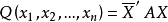的值都是实数。设 a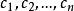是任意不全为零的复数。

1、若恒有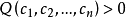，则 Q 称为正定二次型。

2、若恒有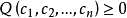，则 Q 称为半正定二次型。

3、若恒有，则 Q 称为负定二次型。

4、若恒有，则 Q 称为半负定二次型。

5、其他情形的 Q 称为不定二次型。

正定、半正定、负定、半负定的埃尔米特二次型统称为定型的；不定的埃尔米特二次型称为不定型的。

埃尔二次型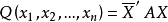是正定的充分必要条件为：Q 的矩阵 A 的各阶顺序主子式都大于零。1

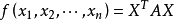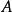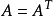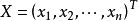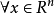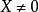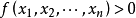正定二次型设，其中矩阵是对称阵，即，为列向量，若，，有，则称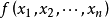为正定二次型，称实对称矩阵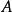正定。1

例如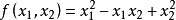，即为正定二次型，其中，。

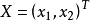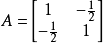本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学